题目内容
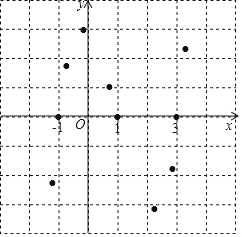
【题目】在平面直角坐标系中,抛物线y=x2的图象如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2019的坐标为_______.

【答案】(-1010,10102)
【解析】
根据二次函数性质可得出点A1的坐标,求得直线A1A2为y=x+2,联立方程求得A2的坐标,即可求得A3的坐标,同理求得A4的坐标,即可求得A5的坐标,根据坐标的变化找出变化规律,即可找出点A2019的坐标.
∵A点坐标为(1,1),
∴直线OA为y=x,A1(-1,1),
∵A1A2∥OA,
∴直线A1A2为y=x+2,
解![]() 得
得![]() 或
或![]() ,
,
∴A2(2,4),
∴A3(-2,4),
∵A3A4∥OA,
∴直线A3A4为y=x+6,
解![]() 得
得![]() 或
或![]() ,
,
∴A4(3,9),
∴A5(-3,9)
…,
∴A2019(-1010,10102),
故答案为(-1010,10102).

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
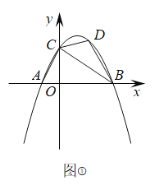
金牌教辅培优优选卷期末冲刺100分系列答案【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如表格:
的图象可以得到如表格:
|
|
|
| + | ﹣ |
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如表表格:
的图象可以得到如表表格:
|
|
|
|
| + | ﹣ | + |
由表格可知不等式![]() 的解集为 .
的解集为 .
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() (x+1)的图象;
(x+1)的图象;
观察函数![]() 的图象补全下面的表格:
的图象补全下面的表格:
|
|
|
|
|
| + | ﹣ |
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
……
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .