题目内容
【题目】(知识背景)
我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定,在十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.
1.(问题初探)
如图(1),△ABC中,∠BAC=90°,AB=AC,点D是BC上一点,连接AD,以AD为一边作△ADE,使∠DAE=90°,AD=AE,连接BE,猜想BE和CD有怎样的数量关系,并说明理由.

2.(类比再探)
如图(2),△ABC中,∠BAC=90°,AB=AC,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作△MDE,使∠DME=90°,MD=ME,连接BE,则∠EBD=________.(直接写出答案,不写过程,但要求作出辅助线)
3.(方法迁移)
如图(3),△ABC是等边三角形,点D是BC上一点,连接AD,以AD为一边作等边三角形ADE,连接BE,则BE、BC之间有怎样的数量关系?________(直接写出答案,不写过程).
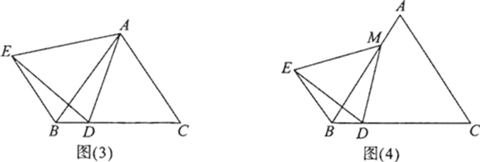
4.(拓展创新)
如图(4),△ABC是等边三角形,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作等边三角形MDE,连接BE.猜想∠EBD的度数,并说明理由.
【答案】【问题初探】BE=CD,理由见解析;【类比再探】![]() ,如图所示,理由见解析;【方法迁移】BE=CD,理由见解析;【拓展创新】
,如图所示,理由见解析;【方法迁移】BE=CD,理由见解析;【拓展创新】![]() ,理由见解析
,理由见解析
【解析】
1.【问题初探】根据已知条件易证得![]() ,从而得到结论;
,从而得到结论;
2.【类比再探】根据四点共圆的判定和性质,即可得到结论;
3.【方法迁移】根据已知条件易证得![]() ,从而得到结论;
,从而得到结论;
4.【拓展创新】根据四点共圆的判定和性质,即可得到结论.
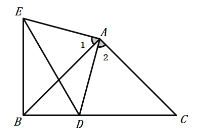
1.【问题初探】BE=CD,理由是:
∵∠EAD=∠BAC=90![]() ,即:∠1+∠BAD=∠2+∠BAD=90
,即:∠1+∠BAD=∠2+∠BAD=90![]() ,
,
∴∠1=∠2
又∵AD=AE,AB=AC,
∴![]() ,
,
∴BE=CD;
2.【类比再探】![]() ,如图所示:
,如图所示:
∵![]() 与
与![]() 都是等腰直角三角形,
都是等腰直角三角形,
∴∠MED=∠MBD=45![]() ,
,
∴B、D、M、E四点共圆,
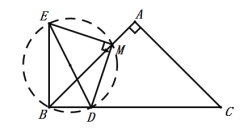
根据圆内接四边形对角互补,
∠EBD=180![]() -∠EMD
-∠EMD![]() ,
,
故答案是:![]() ;
;
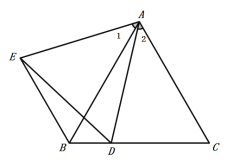
3.【方法迁移】BE=CD,理由是:
∵∠EAD=∠BAC=60![]() ,即:∠1+∠BAD=∠2+∠BAD=60
,即:∠1+∠BAD=∠2+∠BAD=60![]() ,
,
∴∠1=∠2
又∵AD=AE,AB=AC,
∴![]() ,
,
∴BE=CD;
4.【拓展创新】![]() ,理由是:
,理由是:
∵![]() 与
与![]() 都是等边三角形,
都是等边三角形,
∴∠MED=∠MBD=60![]() ,
,
∴B、D、M、E四点共圆,如图所示:
根据圆内接四边形对角互补,
∠EBD=180![]() -∠EMD
-∠EMD![]() ,
,
故答案是:![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案





