题目内容
【题目】矩形ABCD中AB=5,AD=3,将矩形ABCD绕点C顺时针旋转至矩形EFCG(其中A、B、D分别与E、F、G对应).

(1)如图1,当点G落在AB边上时,求AG的长;
(2)如图2.当点G落在线段AE上时,AB与CG交于点H,求BH;
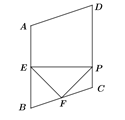
(3)如图3,记O为矩形ABCD的对角线交点,S为△OGE的面积,直接写出s的取值范围.
【答案】(1)1;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)在Rt△BCG中,利用勾股定理求出BG即可解决问题;
(2)首先证明AH=CH,设AH=CH=m,则BH=5m,在Rt△BHC中,根据CH2=BC2+BH2,构建方程求出m即可解决问题;
(3)如图,当点G在对角线AC上时,△OGE的面积最小,当点G在AC的延长线上时,△OE′G′的面积最大,分别求出面积的最小值,最大值即可解决问题.
(1)如图1中,
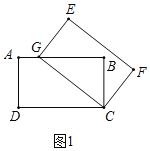
∵四边形ABCD是矩形,
∴AB=CD=CG=5,∠B=90°,
∵BC=AD=3,
∴![]() ,
,
∴AG=AB-BG=1;
(2)如图2中,

由四边形CGEF是矩形,得到∠CGE=90°,
∵点G在线段AE上,
∴∠AGC=90°,
∵CA=CA,CD=CG,
∴Rt△ACG≌Rt△ACD(HL).
∴∠ACD=∠ACG,
∵AB∥CD
∴∠ACD=∠BAC,
∴∠ACG =∠BAC,
∴AH=CH,
设AH=CH=m,
则BH=5-m,
在Rt△BHC中,∵CH2=BC2+BH2,
∴m2=32+(5-m)2,
∴![]() ,
,
∴![]() ;
;
(3)如图,

∵AB=5,AD=3,
∴AC=![]() ,
,
当点G在对角线AC上时,△OGE的面积最小,
最小值 ;
;
当点G在AC的延长线上时,△OE′G′的面积最大,
最大值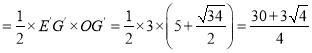
综上所述,![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目