题目内容
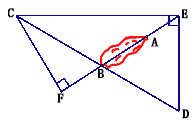
【题目】如图所示,直线y=x+b与双曲线y=![]() (x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(1)求出b、m的值;
(2)点D在x轴的正半轴上,若以点D、C、B组成的三角形与△OAB相似,试求点D的坐标.

【答案】(1)b=﹣4,m=5;(2)D点坐标为:(6,0),(20,0).
【解析】试题分析:(1)将A坐标代入y=x+b,求出b的值,将点A的坐标代入双曲线解析式中,求出m的值即可;(2)如图所示,过点A作AE⊥y轴于点E,根据已知条件易得∠BCD=∠ABO=135°,再求得AB=![]() ,BO=4,BC=4
,BO=4,BC=4![]() ,分△AOB∽BD′C和△AOB∽DBC两种情况求点D的坐标即可.
,分△AOB∽BD′C和△AOB∽DBC两种情况求点D的坐标即可.
试题解析:
(1)∵直线y=x+b的双曲线y=![]() 交于点A(﹣1,﹣5),
交于点A(﹣1,﹣5),
∴﹣1+b=﹣5,m=(﹣1)×(﹣5)=5,
∴解得:b=﹣4,m=5;
(2)如图所示:过点A作AE⊥y轴于点E,
∵CO=OB=4,∠COB=90°,
∴∠OBC=∠OCB=45°,
∴∠ABE=45°,∠BCD=135°,
∴∠ABO=135°,
∵AB=![]() =
=![]() ,BO=4,BC=4
,BO=4,BC=4![]() ,
,
当△AOB∽DBC时,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:CD=2,
∴DO=6,
∴D点坐标为:(6,0);
当△AOB∽BD′C时,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:CD′=16,
∴D′O=16+4=20,
∴D′点坐标为:(20,0),
综上所述,符合要求的D点坐标为:(6,0),(20,0).


练习册系列答案
相关题目