题目内容

如图：Rt△ABC中，∠ACB=90°，过A、C两点的圆O分别交AB、BC于D、E两点，DO⊥AC于H，F为AB上一点，∠A=∠AFE，
（1）求证：EF为⊙O切线；
（2）若AB=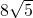 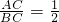$数学公式$ ， $数学公式$ ，求S_△BEF．

（1）证明：连接AE，
∵∠ACE=90°，
∴AE为直径，
∵OA=OD，
∴∠OAD=∠ODA，
又∵∠AFE=∠CAD，
∴∠OAD+∠AFE=∠ODA+∠CAD=90°，
∴∠AEF=90°，
即EF为⊙O切线；

（2）解：连接ED、OC，
∵ $\text{[math]}$ = $\text{[math]}$ ，且AC²+BC²=（8 $\text{[math]}$ ）²，
∴AC=8，BC=16，
∴AH=4，DH=8，
设⊙O半径为R，在Rt△OCH中，
根据勾股定理得：CH²+OH²=OC²，即4²+（8-R）²=R²，
∴R=5，
∴AE=2R=10，
在Rt△ADE中，AD=4 $\text{[math]}$ ，
根据勾股定理得：DE= $\text{[math]}$ =2 $\text{[math]}$ ，
∵Rt△ADE∽Rt△EDF，
∴DE²=DA•DF，
∴DF= $\text{[math]}$ ，BF=3 $\text{[math]}$ ，
则S_△BEF= $\text{[math]}$ BF•ED= $\text{[math]}$ ×3 $\text{[math]}$ ×2 $\text{[math]}$ =15，即S_△BEF=15．
分析：（1）连接AE，由∠ACB=90°，利用90°圆周角所对的弦为直径得到AE为直径，再由OA=OD，利用等边对等角得到一对角相等，再由已知角相等等量代换得到∠OAD与∠AFE互余，即∠AEF为直角，可得出EF为圆O的切线；
（2）由AC与BC的比值，设出AC与BC，再利用勾股定理列出方程，求出AC与BC的长，进而得到AH，DH的值，设圆半径为R，在直角三角形OCH中，根据勾股定理求出R的长，在直角三角形ADE中，由AE，AD的长求出DE的长，由三角形ADE与三角形DEF相似，由相似得比例，求出DF的长，确定出BF的长，由底BF的长，高为DE，利用三角形的面积公式即可求出三角形BEF的面积．
点评：此题考查了切线的判定，勾股定理，相似三角形的判定与性质，以及圆周角定理，熟练掌握切线的判定方法是解本题的关键．