题目内容
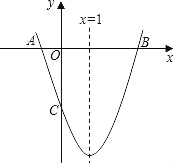
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(﹣1,0)、C(0,﹣3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)(1,﹣2)
【解析】
试题分析:(1)利用待定系数设抛物线的解析式为y=ax2+bx+c,代入求出即可;
(2)根据令x2﹣2x﹣3=0,解得x1=﹣1,x2=3,所以B点坐标为(3,0),进而求出直线BC的解析式,即可得出M点的坐标.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c,
则有: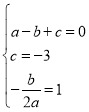 ,
,
解得: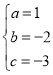
所以抛物线的解析式为y=x2﹣2x﹣3;
(2)令x2﹣2x﹣3=0,解得x1=﹣1,x2=3,所以B点坐标为(3,0).
设直线BC的解析式为y=kx+b,
则![]() ,
,
解得![]() ,
,
所以直线解析式是y=x﹣3.
当x=1时,y=﹣2.
所以M点的坐标为(1,﹣2).

练习册系列答案
相关题目