题目内容
如图,在矩形ABCD中,AB=2AD,线段EF=10.在EF上取一点M,分别以EM、MF为一边作矩形EMNH、矩形MFGN,使矩形MFGN∽矩形ABCD.令MN=x,当x为何值时,矩形EMNH的面积S有最大值,最大值是多少?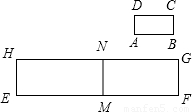
【答案】分析:利用矩形相似,可得到比例线段,先设其中一段,MN=x,再利用面积公式可得到S关于x的二次函数,利用二次函数可求最大值.
解答:解:∵矩形MFGN∽矩形ABCD,
∴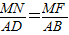 .(1分)
.(1分)
∵AB=2AD,MN=x,
∴MF=2x.(2分)
∴EM=EF-MF=10-2x(0<x<5).
∴S=x(10-2x)(5分)
=-2x2+10x
=-2(x- )2+
)2+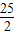 .
.
∴当x= 时,S有最大值为
时,S有最大值为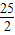 .(8分)
.(8分)
点评:利用矩形相似选择二次函数模型,考查学生在新情境中的知识迁移能力.
同一直线[一分段]上所作的所有平行四边形,其[在整个直线段上平行四边形所余部分形成的]亏形与半线段上一平行四边形相似者,以该半线段上所作且相似于亏形的那个平行四边形(的面积)为最大.
本题实际上是一元二次方程的几何解释,由于考虑到难度的设计,最后将平行四边形相似改成了矩形,将原来要分类讨论的问题改成了只有一种情况.
解答:解:∵矩形MFGN∽矩形ABCD,
∴
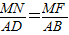 .(1分)
.(1分)∵AB=2AD,MN=x,
∴MF=2x.(2分)
∴EM=EF-MF=10-2x(0<x<5).
∴S=x(10-2x)(5分)
=-2x2+10x
=-2(x-
 )2+
)2+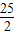 .
.∴当x=
 时,S有最大值为
时,S有最大值为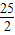 .(8分)
.(8分)点评:利用矩形相似选择二次函数模型,考查学生在新情境中的知识迁移能力.
同一直线[一分段]上所作的所有平行四边形,其[在整个直线段上平行四边形所余部分形成的]亏形与半线段上一平行四边形相似者,以该半线段上所作且相似于亏形的那个平行四边形(的面积)为最大.
本题实际上是一元二次方程的几何解释,由于考虑到难度的设计,最后将平行四边形相似改成了矩形,将原来要分类讨论的问题改成了只有一种情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )



 .
. 动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.
动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象. 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( ) DE,EF与AB交于点F,设CE=x,BF=y.
DE,EF与AB交于点F,设CE=x,BF=y.