题目内容
【题目】如图,已知直线y=![]() x+2交x轴于点A,交y轴于点B,
x+2交x轴于点A,交y轴于点B,
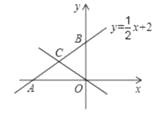
(1)求A,B两点的坐标;
(2)已知点C是线段AB上的一点,当S△AOC= ![]() S△AOB时,求直线OC的解析式。
S△AOB时,求直线OC的解析式。
【答案】(1)点A的坐标为(-4,0),点B的坐标为(0,2);(2)y=-![]() x
x
【解析】
(1)分别令y=0, x=0, 代入一次函数式,即可求出A、B点的坐标;
(2)先由OA和OB的长求出△AOB的面积,设C点坐标为(m,n),△AOC和△AOB等底不同高, 由 S△AOC=![]() S△AOB列式,求出C点的纵坐标n,把n代入一次函数式求出m, 从而得出C点坐标, 设直线OC的解析式为y=kx,根据C点坐标用待定系数法求出k, 即可确定直线OC的函数解析式.
S△AOB列式,求出C点的纵坐标n,把n代入一次函数式求出m, 从而得出C点坐标, 设直线OC的解析式为y=kx,根据C点坐标用待定系数法求出k, 即可确定直线OC的函数解析式.
(1)解:∵直线y= ![]() x+2,
x+2,
∴当x=0时,y=2,当y=0时,x=-4
∵直线y= ![]() x+2交x轴于点A,交y轴于点B,
x+2交x轴于点A,交y轴于点B,
∴点A的坐标为(-4,0),点B的坐标为(0,2)
(2)解:由(1)知,点A的坐标为(-4,0),点B的坐标为(0,2),
∴OA=4,OB=2,
∴S△AOB= ![]() =4
=4
S△AOC= ![]() S△AOB ,
S△AOB ,
∴S△AOC=2
设点C的坐标为(m,n)
∴ ![]() =2,得n=1,
=2,得n=1,
∵点C在线段AB上,
∴1= ![]() m+2,得m=-2
m+2,得m=-2
∴点C的坐标为(-2,1)
设直线OC的解析式为y=kx
-2k=1,得k=- ![]() ,
,
即直线OC的函数解析式为y=-![]() x
x

练习册系列答案
相关题目
【题目】为选拔参加全市中学生数学竞赛的学生,八(2)班组织了一次班内数学竞赛活动,竞赛活动分小组进行,其中甲、乙两组各5人的成绩如下图所示(120分制).

(1)填写下表:
平均数 | 中位数 | |
甲 | ________ | 90 |
乙 | 90 | ________ |
(2)请计算甲、乙两组竞赛成绩的方差,并说明在这次数学竞赛中,哪一组的成绩更为稳定?