Question

【题目】综合与实践

如图，为等腰直角三角形，，点为斜边的中点，是直角三角形，．保持不动，将沿射线向左平移，平移过程中点始终在射线上，且保持直线于点，直线于点．

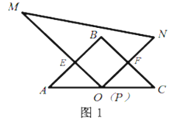
（1）如图1，当点与点重合时，与的数量关系是__________．

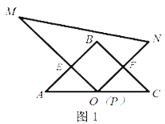
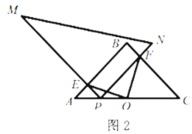
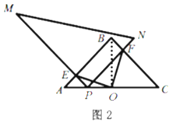
（2）如图2，当点在线段上时，猜想与有怎样的数量关系与位置关系，并对你的猜想结果给予证明；

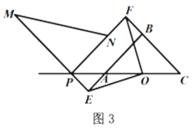
（3）如图3，当点在的延长线上时，连接，若，则的长为__________．

Answer 1

【答案】（1）；（2），，见解析；（3）

【解析】

（1）根据等腰直角三角形的性质证明OA=OC，∠A=∠C,然后证明 ≌即可得到OE=OF；

（2）根据等腰直角三角形的性质证明OA=OB，∠A=∠OBF，利用矩形的判定证明PEBF是矩形，从而得到BF=AE，于是可证明 ≌，即可得到，；

（3）同（2）类似，证明，，然后根据勾股定理即可求出EF的长.

解：（1）=，理由如下：

∵为等腰直角三角形，，点为斜边的中点，

∴OA=OC，∠A=∠C,

∵，，

∴,

∴ ≌,

∴.

故答案是：.

（2）， ，理由如下：

如图2，连接OB，

∵为等腰直角三角形，点为斜边的中点，

∴OA=OB，∠A=∠OBF=, ∠AOB=，

∵，

∴∠A=∠APE=，

∴AE=PE，

∵，，，

∴PEBF是矩形，

∴BF=PE，

∴BF=AE，

在 和中，

，

∴ ≌,

∴，，

∴,

∴.

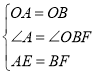故答案是：，.

（3）如图3，连接EF、OB，

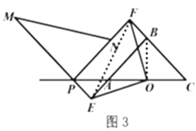
∵为等腰直角三角形，点为斜边的中点，

∴OA=OB，∠BAO=∠OBC=, ∠AOB=，

∴∠EAO=∠OBF=,

∵，

∴∠APE=∠PAE=，

∴AE=PE，

∵，，，

∴PEBF是矩形，

∴BF=PE，

∴BF=AE，

在 和中，

，

∴ ≌,

∴，，

∴,

∴.

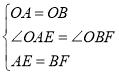∴是等腰直角三角形，

∵OE=1，

∴EF=.

故答案是：.