题目内容
【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在 ![]() 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 .
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 . 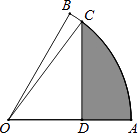
【答案】2π﹣4
【解析】解:∵OC=4,点C在 ![]() 上,CD⊥OA, ∴DC=
上,CD⊥OA, ∴DC= ![]() =
= ![]()
∴S△OCD= ![]() OD
OD ![]()
∴ ![]() =
= ![]() OD2(16﹣OD2)=﹣
OD2(16﹣OD2)=﹣ ![]() OD4+4OD2=﹣
OD4+4OD2=﹣ ![]() (OD2﹣8)2+16
(OD2﹣8)2+16
∴当OD2=8,即OD=2 ![]() 时△OCD的面积最大,
时△OCD的面积最大,
∴DC= ![]() =
= ![]() =2
=2 ![]() ,
,
∴∠COA=45°,
∴阴影部分的面积=扇形AOC的面积﹣△OCD的面积= ![]() ﹣
﹣ ![]() ×2
×2 ![]() ×2
×2 ![]() =2π﹣4,
=2π﹣4,
所以答案是:2π﹣4.
【考点精析】解答此题的关键在于理解二次函数的最值的相关知识,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目
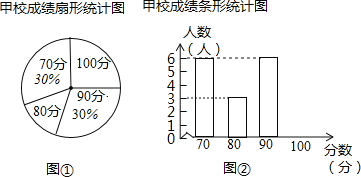
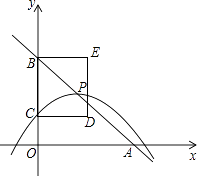
【题目】某市团委举行以“我的中国梦”为主题的知识竞赛,甲、乙两所学校的参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如图不完整的统计图表:
乙校成绩统计表 | |
分数 | 人数 |
70 | 7 |
80 | ______ |
90 | 1 |
100 | 8 |
![]() 乙学校的参赛人数是______人
乙学校的参赛人数是______人![]()
![]() 在图
在图![]() 中,“80分”所在扇形的圆心角度数为______;
中,“80分”所在扇形的圆心角度数为______;
![]() 请你将图
请你将图![]() 补充完整;
补充完整;
![]() 求乙校成绩的平均分.
求乙校成绩的平均分.