ЬтФПФкШн
ЁОЬтФПЁПШчЭМдкГЄЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌби
ЕуГіЗЂЃЌби![]() ТЗЯпдЫЖЏЃЌЕН
ТЗЯпдЫЖЏЃЌЕН![]() ЕуЭЃжЙ;Еу
ЕуЭЃжЙ;Еу![]() Дг
Дг![]() ЕуГіЗЂЃЌби
ЕуГіЗЂЃЌби![]() дЫЖЏЃЌЕН
дЫЖЏЃЌЕН![]() ЕуЭЃжЙШєЕу
ЕуЭЃжЙШєЕу![]() ЁЂЕу
ЁЂЕу![]() ЭЌЪБГіЗЂЃЌЕу
ЭЌЪБГіЗЂЃЌЕу![]() ЕФЫйЖШЮЊУПУы
ЕФЫйЖШЮЊУПУы![]() ЃЌЕу
ЃЌЕу![]() ЕФЫйЖШЮЊУПУы
ЕФЫйЖШЮЊУПУы![]() ЃЌгУ
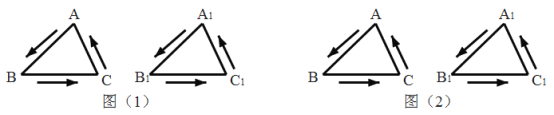
ЃЌгУ![]() ЃЈУыЃЉБэЪОдЫЖЏЪБМфЃЎ
ЃЈУыЃЉБэЪОдЫЖЏЪБМфЃЎ
ЃЈ1ЃЉЕБ![]() __________УыЪБЃЌЕу
__________УыЪБЃЌЕу![]() КЭЕу
КЭЕу![]() ЯргіЃЎ
ЯргіЃЎ
ЃЈ2ЃЉСЌНг![]() ЃЌЕБ
ЃЌЕБ![]() ЦНЗжГЄЗНаЮ
ЦНЗжГЄЗНаЮ![]() ЕФУцЛ§ЪБЃЌЧѓДЫЪБ
ЕФУцЛ§ЪБЃЌЧѓДЫЪБ![]() ЕФжЕ
ЕФжЕ
ЃЈ3ЃЉШєЕу![]() ЁЂЕу
ЁЂЕу![]() дЫЖЏЕН6УыЪБЭЌЪБИФБфЫйЖШЃЌЕу
дЫЖЏЕН6УыЪБЭЌЪБИФБфЫйЖШЃЌЕу![]() ЕФЫйЖШБфЮЊУПУы
ЕФЫйЖШБфЮЊУПУы![]() ЃЌЕу
ЃЌЕу![]() ЕФЫйЖШБфЮЊУПУы
ЕФЫйЖШБфЮЊУПУы![]() ЃЌЧѓдкећИідЫЖЏЙ§ГЬжаЃЌЕу
ЃЌЧѓдкећИідЫЖЏЙ§ГЬжаЃЌЕу![]() Еу
Еу![]() дкдЫЖЏТЗЯпЩЯЯрОрТЗГЬЮЊ
дкдЫЖЏТЗЯпЩЯЯрОрТЗГЬЮЊ![]() ЪБдЫЖЏЪБМф
ЪБдЫЖЏЪБМф![]() ЕФжЕЃЎ
ЕФжЕЃЎ



ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ4Лђ20ЃЛЃЈ3ЃЉ4Лђ14.5
ЃЛЃЈ2ЃЉ4Лђ20ЃЛЃЈ3ЃЉ4Лђ14.5
ЁОНтЮіЁП
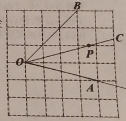
ЃЈ1ЃЉИљОнЕуPдЫЖЏЕФТЗГЬ+ЕуQдЫЖЏЕФТЗГЬ=ШЋГЬГЄЖШЃЌМДПЩЕУГіЙигкxЕФвЛдЊвЛДЮЗНГЬЃЌНтжЎМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЗжЕуPдкABБпЩЯЪБЃЌЕуQдкCDБпЩЯКЭЕуQдЫЖЏЕНAЕуЃЌЕуPдЫЖЏЕНЕуCСНжжЧщПіНјааЬжТлМДПЩЧѓНтЃЎ
ЃЈ3ЃЉЯШЗжЮіБфЫйЧАКЭБфЫйКѓСНжжЧщПіНјааМДПЩЕУЃЎ
ЃЈ1ЃЉИљОнЬтвтЕУЃКx+2x=12ЁС2+8ЃЌ
НтЕУЃКx=![]() ЃЎ
ЃЎ
ЙЪД№АИЃКЕБxЕФжЕЮЊ![]() ЪБЃЌЕуPКЭЕуQЯргіЃЎ
ЪБЃЌЕуPКЭЕуQЯргіЃЎ
ЃЈ2ЃЉЁпPQЦНЗжОиаЮABCDЕФУцЛ§ЃЌ
ЕБЕуPдкABБпЩЯЪБЃЌЕуQдкCDБпЩЯЃЌ
гаЬтвтПЩжЊЃК2x=12xЃЌ
НтЕУЃКx=4ЃЎ
ЕБЕуQдЫЖЏЕНЕуAЪБЃЌгУЪБ(12+8+12)ЁТ2=16УыЃЌДЫЪБЕуPдЫЖЏЕНЕуCЪБЃЌPQЦНЗжОиаЮABCDУцЛ§ЃЌДЫЪБгУЪБЃК(12+8)ЁТ1=20Уы
ЙЪД№АИЃКЕБдЫЖЏ4УыЛђ20УыЪБЃЌPQЦНЗжОиаЮABCDЕФУцЛ§ЃЎ
ЃЈ3ЃЉБфЫйЧАЃКx+2x=32-20
НтЕУx=4
БфЫйКѓЃК12+(x-6)+6+3ЁС(x-6)=32+20
НтЕУx=14.5
злЩЯЫљЪіЃКxЕФжЕЮЊ4Лђ14.5

 аЁбЇЪюМйзївЕЖЋФЯДѓбЇГіАцЩчЯЕСаД№АИ
аЁбЇЪюМйзївЕЖЋФЯДѓбЇГіАцЩчЯЕСаД№АИ НђЧХНЬг§ЪюМйАЮИпЯЮНгЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ
НђЧХНЬг§ЪюМйАЮИпЯЮНгЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ ВЈВЈамЪюМйзївЕНЮїШЫУёГіАцЩчЯЕСаД№АИ
ВЈВЈамЪюМйзївЕНЮїШЫУёГіАцЩчЯЕСаД№АИ бЇЖјгХЪюЦкЯЮНгФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
бЇЖјгХЪюЦкЯЮНгФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ