Question

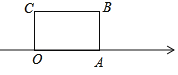
【题目】如图，面积为30的长方形OABC的边OA在数轴上，O为原点，OC=5．将长方形OABC沿数轴水平移动，O，A，B，C移动后的对应点分别记为O1， A1， B1， C1，移动后的长方形O1A1B1C1与原长方形OABC重叠部分的面积记为S

（1）当S恰好等于原长方形面积的一半时，数轴上点A1表示的数是多少?

（2）设点A的移动距离AA1=x

①当S=10时，求x的值；

②D为线段AA1的中点，点E在线段OO1上，且OE=OO1，当点D，E所表示的数互为相反数时，求x的值．

Answer 1

【答案】（1）A1表示的数是3或9；（2）①x=4，②x=.

【解析】

（1）根据长方形的面积可得OA长即点A表示的数，在由已知条件得S=15，根据题意分情况讨论：①当向左移动时，②当向右移动时，根据长方形面积公式分别计算、分析即可得出答案.

（2）①由（1）知：OA=O1A1=6，OC=O1C1=5，由AA1=x得OA1=6-x，由长方形面积公式列出方程，解之即可.

②当向左移动时，由AA1=x得OA1=6-x，OO1=x，根据题意分别得出点E、点D表示的数，由点E和点D表示的数互为相反数列出方程，解之即可；当向右移动时，点D、E表示的数都是正数，不符合题意.

（1）解： ∵S长方形OABC=OA·OC=30，OC=5，

∴OA=6，

∴点A表示的数是6，

∵S= S长方形OABC= ×30=15，

当向左移动时，

OA1·OC=15，

∴OA1=3，

∴A1表示的数是3；

②当向右移动时，

∴O1A·AB=15，

∴O1A=3，

∵OA=O1A1=6，

∴OA1=6+6-3=9，

∴A1表示的数是9；

综上所述：A1表示的数是3或9.

（2）解： ①由（1）知：OA=O1A1=6，OC=O1C1=5，

∵AA1=x，

∴OA1=6-x，

∴S=5×（6-x）=10，

解得：x=4.

②当长方形OABC沿数轴正方向运动时，点D，E表示的数均为正数，不符合题意；
当点D，E所表示的数互为相反数时，长方形OABC沿数轴负方向运动，画图如下：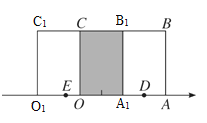

∵AA1=x，

∴OA1=6-x，OO1=x，

∴OE=OO1=x，

∴点E表示的数为-x，

又∵点D为AA1中点，

∴A1D=AA1=x，

∴OD=OA1+A1D=6-x+x=6-x，

∴点D表示的数为6-x，

又∵点E和点D表示的数互为相反数，

∴6-x-x=0，

解得：x=.

故答案为：（1）A1表示的数是3或9；（2）①x=4，②x=.