Question

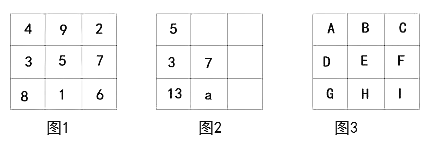
【题目】将9个数填入幻方的九个格中,使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等,如图1所示。

(1)如图2所示,求的值；

(2)如图3所示:

①若求整式D；

②若求这九个整式的和是多少。

Answer 1

【答案】(1)-1;(2)①4a+4；②6a2+18a+9.

【解析】

(1)先根据第一列求出三个数的和，根据这个和求出右下角方格内的数，然后求出第三行中间的数a；

（2）①根据第一行求出三个数的和，和减去对角线的两个数C、E求出G，根据D=和-A-G即可解答；②再根据第一行的三个数的和求出左上角的数，然后求出第一列的第二个数，从而得解．

②根据同一横行、同一竖列、同一斜对角线上的三个数的和相等作出图形，根据题意列出关于a与x的方程，可得x=0，进一步求出这9个数的和即可．

解：（1）（5+3+13）-（5+7）=9，a=（5+3+13）-（13+9）=-1；

（2）①因为G=(A+B+C)-(C+E)=A+B-E=2a+7a+5-(5a+1)=4a+4，D=(A+B+C)-(A+G)=B+C-G=7a+5+6a-2-(4a+4)=9a-1；

②根据上面方法得表格：

根据第一列、第二列的和相等得;

(2a2+6)+( -a2-2a)+( a2+8a+x-3) =( 6a-3)+ (a2-2a-x+6)+( a2+2a)解得：x=0

所以这九个整式的和是：3[(2a2+6)+( -a2-2a)+( a2+8a-3)]=3(2a2+6a+3)= 6a2+18a+9.