题目内容
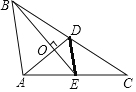
【题目】如图，在△ABC中，AC=6，BC=8，若AC，BC边上的中线BE,AD 垂直相交于点O，则AB=（ ）
A. 5 B. 4
C. 3
D. 2
【答案】D
【解析】
连接DE，根据三角形中线的定义可得E、D分别是AC、BC的中点，由此可得DE是△ABC的中位线，根据中位线的性质可得DE=
AB，接下来根据勾股定理结合图形即可解答.
解：∵BE、AD是△ABC的中线，AC=6，BC=8，
∴E、D分别是AC、BC的中点，BD=CD=4，AE=CE=3，
∴DE是△ABC的中位线，DE=AB，
∵BE⊥AD，
∴BO2+DO2=BD2=16……①，
AO2+EO2+AE2=9……②，
DO2+EO2=DE2=
AB2……③，
BO2+AO2=AB2……④，
∵①+②=BO2+DO2+AO2+EO2，③+④= BO2+DO2+AO2+EO2，
∴①+②=③+④，
∴16+9=AB2+AB2，
∴AB=2
.
故选D.
练习册系列答案
阅读快车系列答案
相关题目
