题目内容
【题目】如图,在长方形ABCD中,AB=8,AD=10,点E为BC上一点,将△ABE沿AE折叠,使点B落在长方形内点F处,且DF=6.
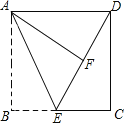
(1)试说明:△ADF是直角三角形;
(2)求BE的长.
【答案】(1)见解析;(2)BE=4.
【解析】
(1)由折叠的性质可知AF=AB=8,然后再依据勾股定理的逆定理可证明△ADF为直角三角形;
(2)由题意可证点E、D、F在一条直线上,设BE=x,则EF=x,DE=6+x,EC=10-x,在Rt△CED中,依据勾股定理列方程求解即可.
(1)将△ABE沿AE折叠,使点B落在长方形内点F处,
∴AF=AB=8,
∵AF2+DF2=62+82=100=102=AD2,
∴∠AFD=90°
∴△ADF是直角三角形
(2)∵折叠
∴BE=EF,∠B=∠AFE=90°
又∵∠AFD=90°
∴点D,F,E在一条直线上.
设BE=x,则EF=x,DE=6+x,EC=10-x,
在Rt△DCE中,∠C=90°,
∴CE2+CD2=DE2,
即(10-x)2+82=(6+x)2.
∴x=4.
∴BE=4.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目