题目内容
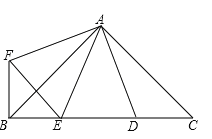
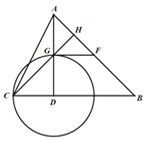
【题目】如图，在△ABC中，∠B=45°，AD⊥BC于点D，以D为圆心DC为半径作⊙D交AD于点G，过点G作⊙D的切线交AB于点F，且F恰好为AB中点.
（1）求tan∠ACD的值.
（2）连结CG并延长交AB于点H，若AH=2，求AC的长.
【答案】（1）2；（2）
【解析】解：（1）∵FG与⊙D相切 ∴∠DGF=90°∵AD⊥BC
∴FG∥CB∵F为AB中点∴ 
∴AD=2GD=2CD∴tan∠ACD=2
（2）∵AD⊥BC∴∠ADB=90° ∵∠B=45°∴△ADB是等腰直角三角形∴∠DAB=45°
∵GD=CD，∠GDC=90°∴△CGD是等腰直角三角形∴∠GCD=45°
∴∠AHC=90° ∴△AGH是等腰直角三角形∵AH=2,∴HG=2,
∴GD=
∴CG=4∴HC=6∴
练习册系列答案
相关题目
