题目内容
【题目】Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于![]() EF为半径画弧,两弧交于点N,若BC=
EF为半径画弧,两弧交于点N,若BC=![]() , 则点M到AC的距离是( )
, 则点M到AC的距离是( )
A.1
B.![]()
C.![]()
D.3
【答案】A
【解析】解:∵在Rt△ABC中,∠B=90°∠A=30°,
∴∠ACB=60°,
∵以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于![]() EF为半径画弧,两弧交于点N,
EF为半径画弧,两弧交于点N,
∴∠ACM=∠MCB=30°,
∵∠B=90°,
∴CM=2BM,
∵BC=![]() ,
,
∴由勾股定理得:BM2+(![]() )2=(2BM)2 ,
)2=(2BM)2 ,
解得:BM=1,
∵∠B=90°,∠ACM=∠BCM,
∴点M到AC的距离等于BM的长,即是1,
故选A.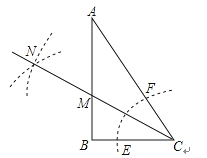
【考点精析】关于本题考查的角平分线的性质定理,需要了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能得出正确答案.

练习册系列答案
相关题目

