题目内容
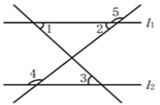
【题目】如图所示，直线EF与直线AB、CD相交于点M和点N，MG、NH分别平分∠AMN和∠MND，并且∠1＝∠2，由这些条件能得出AB平行于CD吗？能得出MG平行于NH吗？
【答案】能理由：见解析
【解析】试题分析：首先根据角平分线的性质可知∠1＝
∠AMN，∠2＝
∠MND，根据条件∠1=∠2，可得∠AMN＝∠MND，根据内错角相等，两直线平行可证明AB∥CD．由∠1＝∠GMN，∠2＝∠MNH，得到∠GMN＝∠MNH，根据内错角相等，两直线平行可证明MG∥NH．
试题解析：解：能．理由如下：
∵MG、NH分别平分∠AMN和∠MND，∴∠1＝
∠AMN，∠2＝
∠MND（角平分线的定义）．
∵∠1＝∠2，∴∠AMN＝∠MND（等量代换），∴AB∥CD（内错角相等，两直线平行）．
∵∠1＝∠GMN，∠2＝∠MNH（角平分线的定义），∴∠GMN＝∠MNH（等量代换），∴MG∥NH（内错角相等，两直线平行）．
练习册系列答案
相关题目
