题目内容
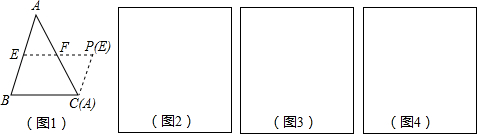
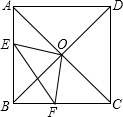 如图示,正方形ABCD中,E、F分别在AB、BC上,AC、BD交于O点且AC⊥BD,∠EOF=90°,已知AE=3,CF=4,则S△BEF为________.
如图示,正方形ABCD中,E、F分别在AB、BC上,AC、BD交于O点且AC⊥BD,∠EOF=90°,已知AE=3,CF=4,则S△BEF为________.
6
分析:求出∠EOB=∠FOC,∠EBO=∠FCO,根据OB=OC,利用ASA证△EBO≌△FCO,推出BE=CF=4,求出AB=7,BF=3,代入三角形面积公式求出即可.
解答:∵AC⊥BD,∠EOF=90°,
∴∠EOF=∠BOC=90°,
∴∠EOF-∠BOF=∠BOC-∠BOF,
∴∠EOB=∠FOC,
∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,
在△EBO和△FCO中
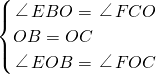 ,
,
∴△EBO≌△FCO(ASA),
∴BE=CF=4,
∴AB=BE+AE=4+3=7,
∴BF=7-4=3,
∴S△BEF= ×BE×BF=
×BE×BF= ×4×3=6,
×4×3=6,
故答案为:6.
点评:本题考查了正方形性质,全等三角形的性质和判定等知识点,关键是证出△EBO≌△FCO后求出BE=CF=4,题目比较好.
分析:求出∠EOB=∠FOC,∠EBO=∠FCO,根据OB=OC,利用ASA证△EBO≌△FCO,推出BE=CF=4,求出AB=7,BF=3,代入三角形面积公式求出即可.
解答:∵AC⊥BD,∠EOF=90°,
∴∠EOF=∠BOC=90°,
∴∠EOF-∠BOF=∠BOC-∠BOF,
∴∠EOB=∠FOC,
∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,
在△EBO和△FCO中
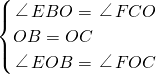 ,
,∴△EBO≌△FCO(ASA),
∴BE=CF=4,
∴AB=BE+AE=4+3=7,
∴BF=7-4=3,
∴S△BEF=
 ×BE×BF=
×BE×BF= ×4×3=6,
×4×3=6,故答案为:6.
点评:本题考查了正方形性质,全等三角形的性质和判定等知识点,关键是证出△EBO≌△FCO后求出BE=CF=4,题目比较好.

练习册系列答案
相关题目
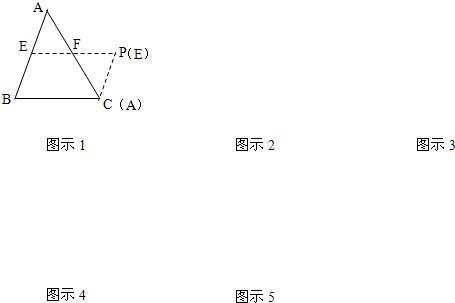
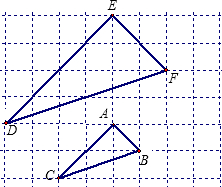 FD的三个顶点都在格点上,如果△EFD是由△ABC经过平移与位似两次几何变换得到的.
FD的三个顶点都在格点上,如果△EFD是由△ABC经过平移与位似两次几何变换得到的.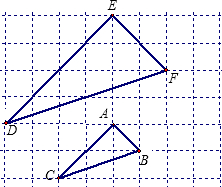 FD的三个顶点都在格点上,如果△EFD是由△ABC经过平移与位似两次几何变换得到的.
FD的三个顶点都在格点上,如果△EFD是由△ABC经过平移与位似两次几何变换得到的.