题目内容
【题目】如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB. 
(1)求证:PB是⊙O的切线;
(2)若PC=9,AB=6 ![]() , ①求图中阴影部分的面积;
, ①求图中阴影部分的面积;
【答案】
(1)证明:如图1,连接OB,
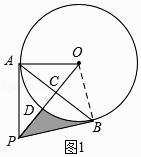
∵OP⊥AB,OP经过圆心O,
∴AC=BC,
∴OP垂直平分AB,
∴AP=BP,
∵OA=OB,OP=OP,
∴△APO≌△BPO(SSS),
∴∠PAO=∠PBO,
∵PA切⊙O于点A,
∴AP⊥OA,
∴∠PAO=90°,
∴∠PBO=∠PAO=90°,
∴OB⊥BP,
又∵点B在⊙O上,
∴PB与⊙O相切于点B;
(2)解:如图1,

∵OP⊥AB,OP经过圆心O,
∴BC= ![]() AB=3
AB=3 ![]() ,
,
∵∠PBO=∠BCO=90°,
∴∠PBC+∠OBC=∠OBC+∠BOC=90°,
∴∠PBC=∠BOC,
∴△PBC∽△BOC,
∴ ![]()
∴OC= ![]() =
= ![]() =3,
=3,
∴在Rt△OCB中,OB= ![]() =
= ![]() =6,tan∠COB=
=6,tan∠COB= ![]() =
= ![]() ,
,
∴∠COB=60°,
∴S△OPB= ![]() ×OP×BC=
×OP×BC= ![]() ×
× ![]() =18
=18 ![]() ,S扇DOB=
,S扇DOB= ![]() =6π,
=6π,
∴S阴影=S△OPB﹣S扇DOB=18 ![]() ﹣6π;
﹣6π;
②若点E是⊙O上一点,连接AE,BE,当AE=6 ![]() 时,BE= .
时,BE= .
3 ![]() ﹣3
﹣3 ![]() 或3
或3 ![]() +3
+3 ![]()
【解析】②分两种情况: i)当点E在 ![]() 上时,如图2,作直径AF,交⊙O于F,连接EF、EB,过O作OG⊥AE于G,过F作FH⊥EB于H,
上时,如图2,作直径AF,交⊙O于F,连接EF、EB,过O作OG⊥AE于G,过F作FH⊥EB于H,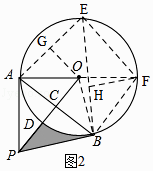
∴EG=AG= ![]() AE=
AE= ![]() ×
× ![]() =3
=3 ![]() ,
,
∵∠AOB=120°,OA=OB,
∴∠OAB=30°,
∴∠BEF=∠OAB=30°,
Rt△OGE中,由①知:OA=6,
∴OG= ![]() =
= ![]() =3
=3 ![]() ,
,
∴AG=OG,
∴△OGA是等腰直角三角形,
∴∠OAE=45°,
∴∠EBF=∠OAE=45°,
∵AF是⊙O的直径,
∴∠AEF=90°,
∴△AEF是等腰直角三角形,
∴EF=AE=6 ![]() ,
,
Rt△EHF中,∠BEF=30°,
∴FH= ![]() EF=3
EF=3 ![]() ,
,
∴EH= ![]() =
= ![]() =3
=3 ![]() ,
,
Rt△BHF中,∵∠EBF=45°,
∴△BHF是等腰直角三角形,
∴BH=FH=3 ![]() ,
,
∴BE=3 ![]() +3
+3 ![]() ,
,
ii)当点E在劣弧 ![]() 上时,如图3,
上时,如图3,
作直径AF,并⊙O于F,连接OB、OE、BF,过B作BH⊥OE于H,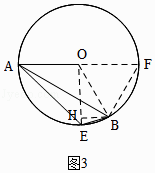
∵AF为⊙O的直径,
∴∠ABF=90°,
∵∠BAF=30°,
∴∠F=∠BOF=60°,
∵OA=OE=6,AE=6 ![]() ,
,
∴OA2+OE2=AE2 ,
∴∠AOE=90°,
∴∠EOF=90°,
∴∠EOB=30°,
Rt△OHB中,BH= ![]() OB=3,
OB=3,
∴OH= ![]() =3
=3 ![]() ,
,
∴EH=6﹣3 ![]() ,
,
∴BE= ![]() =
= ![]() =
= ![]() =3
=3 ![]() ﹣3
﹣3 ![]() ;
;
综上所述,BE的长为3 ![]() +3
+3 ![]() 或3
或3 ![]() ﹣3
﹣3 ![]() ;
;
所以答案是:3 ![]() ﹣3
﹣3 ![]() 或3
或3 ![]() +3
+3 ![]() .
.
【考点精析】通过灵活运用垂径定理和扇形面积计算公式,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分球投篮测试,每人每次投10个球,图记录的是这两名同学5次投篮所投中的个数.

(1)请你根据图中的数据,填写下表;
姓名 | 平均数 | 众数 | 方差 |
王亮 | 7 | ||
李刚 | 7 | 2.8 |
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.