题目内容
【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,
(1)当点E为AB的中点时,如图1,求证:EC=ED; 
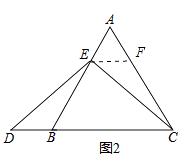
(2)当点E不是AB的中点时,如图2,过点E作EF∥BC,求证:△AEF是等边三角形; 
(3)在第(2)小题的条件下,EC与ED还相等吗,请说明理由.
【答案】
(1)证明:如图1,在等边△ABC中,AB=BC=AC,
∴∠ABC=∠ACB=∠A=60°,
∵AE=EB=BD,
∴∠ECB= ![]() ∠ACB=30°,∠EDB=∠DEB=
∠ACB=30°,∠EDB=∠DEB= ![]() ∠ACB=30°,
∠ACB=30°,
∴∠EDB=∠ECB,
∴EC=ED
(2)证明:如图2,∵EF∥BC,
∴∠AEF=∠ABC=60°,∠AFE=∠C=60°,
∴△AEF为等边三角形
(3)证明:EC=ED;
理由:∵∠AEF=∠ABC=60°,
∴∠EFC=∠DBE=120°,
∵AB=AC,AE=AF,
∴AB﹣AE=AC﹣AF,即BE=FC,
在△DBE和△EFC中,
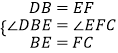 ,
,
∴△DBE≌△EFC(SAS),
∴ED=EC.
【解析】(1)根据等边三角形三线合一的性质可得∠ECB=30°,∠ABC=60°,根据AE=EB=BD,可得∠ECB= ![]() ∠ACB=30°,∠EDB=∠DEB=
∠ACB=30°,∠EDB=∠DEB= ![]() ∠ACB=30°,根据等角对等边即可证得结论;(2)根据平行线的性质证得∠AEF=∠ABC=60°,∠AFE=∠C=60°,即可证得结论;(3)先求得BE=FC,然后证得△DBE≌△EFC即可;
∠ACB=30°,根据等角对等边即可证得结论;(2)根据平行线的性质证得∠AEF=∠ABC=60°,∠AFE=∠C=60°,即可证得结论;(3)先求得BE=FC,然后证得△DBE≌△EFC即可;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





