题目内容
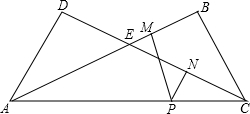 如图,将矩形纸片ABCD沿对角线AC折叠,AB与CD交于点E.
如图,将矩形纸片ABCD沿对角线AC折叠,AB与CD交于点E.(1)若AB=8,AD=4,求AE的长;
(2)点P为线段AC上的任意一点,PM⊥AB于M,PN⊥CD于N,若PM+PN=4,DE=3,求△AEC的面积.
分析:(1)先补全矩形,再根据翻折的性质可得∠BAC=∠B′AC,再根据矩形的对边互相平行可得AB′∥CD,根据两直线平行,内错角相等可得∠B′AC=∠ACD,从而得到∠ACD=∠BAC,根据等角对等边可得AE=CE,设AE=CE=x,表示出DE,然后在Rt△ADE中,利用勾股定理列出方程求解即可;
(2)过点P作PM′⊥AB′于M′,根据角平分线上的点到角的两边的距离相等可得PM=PM′,然后根据等角的余角相等求出∠APM′=∠CPN,判断出点M′、P、N三点共线,从而得到AD=PM+PN,再利用勾股定理列式求出AE,最后利用三角形的面积公式列式计算即可得解.
(2)过点P作PM′⊥AB′于M′,根据角平分线上的点到角的两边的距离相等可得PM=PM′,然后根据等角的余角相等求出∠APM′=∠CPN,判断出点M′、P、N三点共线,从而得到AD=PM+PN,再利用勾股定理列式求出AE,最后利用三角形的面积公式列式计算即可得解.
解答:解:(1)补全矩形ABCD如图所示,
由翻折的性质得,∠BAC=∠B′AC,
∵矩形ABCD的边AB′∥CD,
∴∠B′AC=∠ACD,
∴∠ACD=∠BAC,
∴AE=CE,
设AE=CE=x,
则DE=CD-CE=AB-CE=8-x,
在Rt△ADE中,AD2+DE2=AE2,
即42+(8-x)2=x2,
解得x=5,
∴AE=5;
(2)过点P作PM′⊥AB′于M′,
∵∠BAC=∠B′AC,PM⊥AB,
∴PM=PM′,
∵PN⊥CD,
∴∠ACD+∠CPN=90°,
又∵∠B′AC+∠APM′=90°,
∴∠APM′=∠CPN,
∴M′、P、N三点共线,
∵PM+PN=4,
∴PM+PN=PM′+PN=AD=4,
在Rt△ADE中,AE=
=
=5,
∴CE=AE=5,
∴△AEC的面积=
CE•AD=
×5×4=10.
由翻折的性质得,∠BAC=∠B′AC,
∵矩形ABCD的边AB′∥CD,
∴∠B′AC=∠ACD,
∴∠ACD=∠BAC,
∴AE=CE,
设AE=CE=x,
则DE=CD-CE=AB-CE=8-x,
在Rt△ADE中,AD2+DE2=AE2,
即42+(8-x)2=x2,
解得x=5,

∴AE=5;
(2)过点P作PM′⊥AB′于M′,
∵∠BAC=∠B′AC,PM⊥AB,
∴PM=PM′,
∵PN⊥CD,
∴∠ACD+∠CPN=90°,
又∵∠B′AC+∠APM′=90°,
∴∠APM′=∠CPN,
∴M′、P、N三点共线,
∵PM+PN=4,
∴PM+PN=PM′+PN=AD=4,
在Rt△ADE中,AE=
| AD2+DE2 |
| 42+32 |
∴CE=AE=5,
∴△AEC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了翻折变换,矩形的性质,勾股定理的应用,角平分线上的点到角的两边的距离相等的性质,作辅助线构造出矩形,并求出PM+PN的长度等于矩形的边AD的长是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 23、如图,将矩形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
23、如图,将矩形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.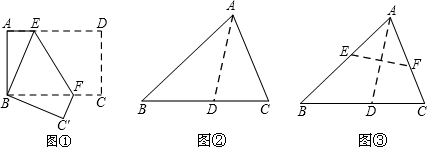
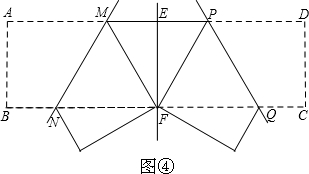
 (2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( )
(2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( ) 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
