题目内容
【题目】如图，AB为⊙O的直径，C在⊙O上，并且OC⊥AB，P为⊙O上的一点，位于B、C之间，直线CP与AB相交于点Q，过点Q作直线与AB垂直，交直线AP于R．求证：BQ=QR．
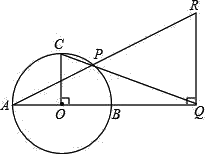
【答案】见解析
【解析】
连接BR、BP，由圆周角定理知∠APB=∠AQR=90°，由此可得B、P、R、Q四点共圆，由圆周角定理知∠BPQ=∠BRQ；而∠BPQ是∠CPB的补角，由此可求得∠BPQ=45°，即∠BRQ=45°，可得△BQR是等腰Rt△，由此得证．
如图，连接PB、BR，
则∠APC=45°，∠APB=90°，
故∠BPQ=180°﹣∠APC﹣∠APB=45°，
又∵∠APB=90°=∠BQR，
∴B、Q、R、P四点共圆，
于是∠BRQ=∠BPQ=45°，
从而△BQR为等腰直角三角形，
∴BQ=QR．
练习册系列答案
相关题目
【题目】“十九大”报告提出“实施健康中国战略”，其中雾霾天气成为环保和健康问题的焦点，为了调查学生对雾霾天气知识的了解程度，某中学在全校学生中抽取部分同学做了一次调查，根据调查结果，绘制了如下不完整的统计图表．
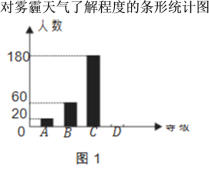
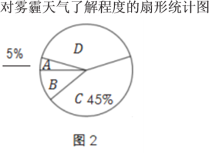
对雾霾天气了解程度的统计表
对雾霾天气知识 | 百分比 |
A． 非常了解 | 5% |
B． 比较了解 | m |
C． 基本了解 | 45% |
D． 不了解 | n |
请结合统计图表，回答下列问题：
（1）统计表中：m=__________，n=__________；
（2）请补全图1中的条形统计图；
（3）在图2所示的扇形统计图中，求D所在扇形对应的圆心角是多少度？
