题目内容
【题目】如图,在Rt△ABC中,∠BAC=90°,AB>AC , 射线AM平分∠BAC . 
(1)设AM交BC于点D , 作DE⊥AB于点E , DF⊥AC于点F , 连接EF . 有以下三种“判断”:
判断1:AD垂直平分EF.
判断2:EF垂直平分AD.
判断3:AD与EF互相垂直平分.
你同意哪个“判断”?简述理由;
(2)若射线AM上有一点N到△ABC的顶点B , C的距离相等,连接NB , NC .
①请指出△NBC的形状,并说明理由;
②当AB=11,AC=7时,求四边形ABNC的面积.
【答案】
(1)
解:判断3.理由如下:如图,

∵DE⊥AB于点E,DF⊥AC于点F, ∠BAC=90°,
∴四边形AEDF是矩形,
又∵射线AM平分∠BAC,
∴∠DAE=∠DAF,
又∵AEDF是矩形,
∴AF//DE,
∴∠DAF=∠EDA。
∴∠EDA=∠DAE,
则AE=DE,
则矩形AEDF是正方形。
即AD与EF互相垂直平分.
(2)
解:①等腰直角三角形.理由如下:
作NE⊥AB于点E,NF⊥AC于点F,
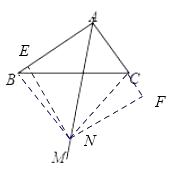
由(1)可得四边形AENF是正方形,
∴NE=NF,∠ENF=∠NEA=∠NFC=90°,
∴∠NEB=∠NFC=90°,
又NB=NC,
则△NBE≌△NCF,
∴∠BNE=∠CNF,
∴∠BNC=∠ENF=90°,
∴△NBC是等腰直角三角形.
②在Rt△ABC中,由勾股定理得BC=![]() .
.
在Rt△NBC中,∵NB=NC,BC=![]() ,
,
则NB=NC=![]() =
=![]() ,
,
则四边形ABNC的面积=S△ABC+S△NBC=![]() ×11×7+
×11×7+![]() ×
×![]() ×
×![]() =
=![]() ×162=81.
×162=81.
【解析】(1)判断四边形AEDF为正方形,即可证明;
(2)①根据(1)中的方法作出两条垂线,则可证得NE=NF,∠ENF=∠NEA=∠NFC=90°,再证明△NBE≌△NCF,通过等量代换,证明∠BNC=∠ENF=90°;
②由勾股定理求出△NBC直角边的长度分别计算S△ABC和S△NBC即可求得答案.
【考点精析】关于本题考查的等腰直角三角形和勾股定理的概念,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.