题目内容
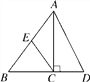
【题目】如图,在△ABD中,AC⊥BD于点C, ![]() ,点E是AB的中点,tanD=2,CE=1,求sin∠ECB的值和AD的长.
,点E是AB的中点,tanD=2,CE=1,求sin∠ECB的值和AD的长.
【答案】sin∠ECB=![]() , AD=
, AD=![]() .
.
【解析】试题分析:由直角三角形斜边上的中线等于斜边的一半,得到AB=2,设BC=3x,则CD=2x,AC=4x,在Rt△ACB中由勾股定理AB=5x,由∠ECB=∠B,求出sin∠ECB及x的值,在Rt△ACD中,由勾股定理求得AD的长.
试题解析:∵AC⊥BD,∴∠ACB=∠ACD=90°,∵点E是AB的中点,CE=1,∴BE=CE=1,AB=2CE=2,∴∠B=∠ECB,
∵![]() ,∴设BC=3x,CD=2x,
,∴设BC=3x,CD=2x,
在Rt△ACD中,tanD=2,∴ ![]() ,∴AC=4x,
,∴AC=4x,
在Rt△ACB中,由勾股定理得AB=![]() =5x,∴sin∠ECB=sinB=
=5x,∴sin∠ECB=sinB=![]() =
=![]() ,由AB=2,得x=
,由AB=2,得x=![]() ,
,
∴AD=![]() =
=![]() =2
=2 ![]() =2
=2![]() ×
×![]() =
=![]() .
.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】某校教师开展了“练一手好字”的活动,校委会对部分教师练习字帖的情况进行了问卷调查,问卷设置了“柳体”、“颜体”、”欧体“和”其他“类型,每位教师仅能选一项,根据调查的结果绘制了如下统计表:
类别 | 柳体 | 颜体 | 欧体 | 其他 | 合计 |
人数 | 4 | 10 | 6 | ||
占的百分比 | 0.5 | 0.25 | 1 |
根据图表提供的信息解答下列问题:
(1)这次问卷调查了多少名教师?
(2)请你补全表格.
(3)在调查问卷中,甲、乙、丙、丁四位教师选择了“柳体”,现从以上四位教师中任意选出2名教师参加学校的柳体兴趣小组,请你用画树状图或列表的方法,求选出的2人恰好是乙和丙两位教师的概率.