Question

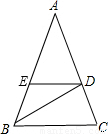
已知△ABC中，AB=AC，∠A=36°，点D在AC上，将△BDC绕点D按顺时针方向旋转α（0°＜α＜180°），使△BDC与△ADE重合（如图所示）．
（1）求角α；
（2）说明四边形EBCD是等腰梯形．

Answer 1

【答案】分析：（1）首先明确题意，要求α，即求∠ADB的度数．已知△BDC与△ADE重合，易求α．
（2）根据第一问的答案证明∠ABC=∠C，即可证得四边形EBCD为等腰梯形．
解答：解：（1）∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵△BDC与△ADE重合，
∴∠DBC=∠A=36°，∠AED=∠C=72°，
∴∠ADE=∠BDC=180°-（72°+36°）=72°，
∴α=180°-∠BDC=180°-72°=108°．

（2）由（1）∠ADE=∠C=72°，
∴DE∥BC，又BE与CD不平行，
∴四边形EBCD是梯形，
∵∠ABC=∠C=72°，
∴四边形EBCD是等腰梯形．
点评：本题考查的是等腰梯形的判定定理，等腰三角形的性质．值得注意的是考生应掌握好各角之间的关系方可求解．