题目内容
已知△ABC中,AB=20,AC=15,BC边上的高为12,则△ABC的周长为分析:此题分两种情况:∠B为锐角或∠C为钝角.△ABC的周长为AB+AC+BC,已知AB、AC的值,所以要求三角形的周长,只需求出BC的值即可.如下图所示:作AD⊥BC于D,则AD为BC边上的高,在Rt△ADC中,由勾股定理得:AC2=AD2+DC2,在Rt△ADB中,由勾股定理得:AB2=AD2+BD2,代入AB=20,AC=15,AD=12,可求出BD、DC的值,BC=BD+DC,将AB、BC、AC的值代入周长公式,可求出该三角形的周长.
解答:解:作AD⊥BC于D,则AD为BC边上的高,AD=12.分两种情况:
①高AD在三角形内,如图所示: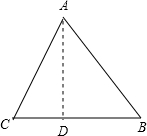 在Rt△ADC中,由勾股定理得:
在Rt△ADC中,由勾股定理得:
AC2=AD2+DC2,
∴DC=
=
=9,
在Rt△ADB中,由勾股定理得:
AB2=AD2+BD2,
∴BD=
=
=16,
∴BC=BD+DC=16+9=25,
所以,△ABC的周长为AB+AC+BC=20+15+25=60.
②高AD在三角形外,如图所示:
在Rt△ADC中,由勾股定理得:
AC2=AD2+DC2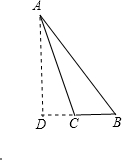
∴DC=
=
=9,
在Rt△ADB中,由勾股定理得:
AB2=AD2+BD2,
∴BD=
=
=16,
∴BC=BD-DC=16-9=7,
所以,△ABC的周长为AB+AC+BC=20+15+7=42.
故△ABC的周长为60或42.
①高AD在三角形内,如图所示:
 在Rt△ADC中,由勾股定理得:
在Rt△ADC中,由勾股定理得:AC2=AD2+DC2,
∴DC=
| AC2-AD2 |
| 152-122 |
在Rt△ADB中,由勾股定理得:
AB2=AD2+BD2,
∴BD=
| AB2-AD2 |
| 202-122 |
∴BC=BD+DC=16+9=25,
所以,△ABC的周长为AB+AC+BC=20+15+25=60.
②高AD在三角形外,如图所示:
在Rt△ADC中,由勾股定理得:
AC2=AD2+DC2

∴DC=
| AC2-AD2 |
| 152-122 |
在Rt△ADB中,由勾股定理得:
AB2=AD2+BD2,
∴BD=
| AB2-AD2 |
| 202-122 |
∴BC=BD-DC=16-9=7,
所以,△ABC的周长为AB+AC+BC=20+15+7=42.
故△ABC的周长为60或42.
点评:本题主要考查运用勾股定理结合三角形的周长公式求三角形周长的能力,三角形的周长等于三边之和.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由. 已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高,
已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高, 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
 如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.
如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.