题目内容
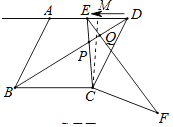
【题目】如图1.在菱形ABCD中,AB=2 ![]() ,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.
,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.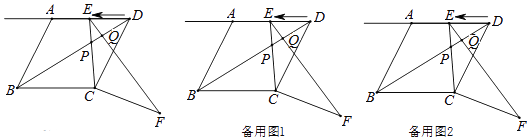
(1)求证:△ECF∽△BCD;
(2)当t为何值时,△ECF≌△BCD?
(3)当t为何值时,△EPQ是直角三角形?
【答案】
(1)
证明:菱形ABCD中,BC=CD,
由旋转的性质可知,CE=CF,
∴ ![]() =
= ![]() ,
,
又∵∠FCE=∠DCB=α,
∴△FCE∽△DCB
(2)
由(1)知,△FCE∽△DCB,
∴当CE=CB=CD时,△FCE≌△DCB;
①E、D重合,此时t=0;
②如图,过点C作CM⊥AD,
当EM=MD时,EC=CD,
Rt△CMD中,MD=CDcos∠CDA=2 ![]() ×
× ![]() =2,
=2,
∴t=ED=2MD=4,
∴当t=0或4时,△FCE≌△DCB
(3)
∵CE=CF,∴∠CEQ<90°.
①当∠EQD=90°时,
∠ECF=∠BCD,BC=DC,EC=FC,
∴∠CBD=∠CEF,
∵∠BPC=∠EPQ,
∴∠BCP=∠EQP=90°.
在Rt△CDE中,∠CED=90°,
∵AB=CD=2 ![]() ,tan∠ABC=tan∠ADC=2,
,tan∠ABC=tan∠ADC=2,
∴DE=2,
∴t=2秒;
②当∠EPQ=90°时,
∵菱形ABCD对角线AC⊥BD,
∴EC和AC重合.
∴DE=2 ![]() ,
,
∴t=2 ![]() 秒;
秒;
∴当t=2或者2 ![]() 时,△APQ为直角三角形.
时,△APQ为直角三角形.
【解析】(1)根据对应边成比例、夹角相等的两个三角形相似证明;(2)根据全等三角形的性质、余弦的概念计算;(3)分∠EQD=90°、∠EPQ=90°两种情况,根据正切的概念、菱形的性质解答.
【考点精析】解答此题的关键在于理解相似图形的相关知识,掌握形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例.