Question

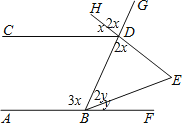
【题目】如图，已知直线AB∥CD，点F为直线AB上一点，G为射线BD上一点．若∠HDG＝2∠CDH，∠GBE＝2∠EBF，HD交BE于点E，则∠E的度数为（　　）

A.45B.60°C.65°D.无法确定

Answer 1

【答案】B

【解析】

设∠CDH＝x，∠EBF＝y，得到∠HDG＝2x，∠DBE＝2y，根据平行线的性质得到∠ABD＝∠CDG＝3x，求得x+y＝60°，根据三角形的内角和即可得到结论．

解：∵∠HDG＝2∠CDH，∠GBE＝2∠EBF，

∴设∠CDH＝x，∠EBF＝y，

∴∠HDG＝2x，∠DBE＝2y，

∵AB∥CD，

∴∠ABD＝∠CDG＝3x，

∴3x+2y+y＝180°，

∴x+y＝60°，

∵∠BDE＝∠HDG＝2x，

∴∠E＝180°﹣2x﹣2y＝180°﹣2（x+y）＝60°，

故选：B．