题目内容
【题目】(1)阅读理解:
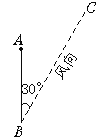
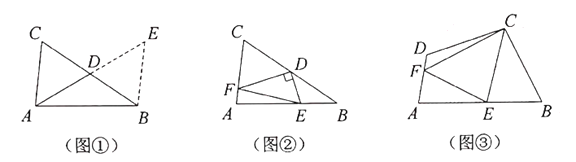
如图①,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
可以用如下方法:将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,在
,在![]() 中,利用三角形三边的关系即可判断中线
中,利用三角形三边的关系即可判断中线![]() 的取值范围是______;
的取值范围是______;
(2)问题解决:
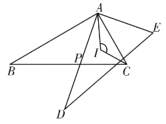
如图②,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)问题拓展:
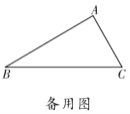
如图③,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作一个
为顶点作一个![]() 的角,角的两边分别交
的角,角的两边分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,探索线段
,探索线段![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)![]() ;(2)见详解;(3)
;(2)见详解;(3)![]() ,理由见详解
,理由见详解
【解析】
(1)根据旋转的性质可证明![]() ,
,![]() ,在
,在![]() 中根据三角形三边关系即可得出答案;
中根据三角形三边关系即可得出答案;
(2)延长FD至M,使DF=DM,连接BM,EM,可得出![]() ,根据垂直平分线的性质可得出
,根据垂直平分线的性质可得出![]() ,利用三角形三边关系即可得出结论;
,利用三角形三边关系即可得出结论;
(3)延长AB至N,使BN=DF,连接CN,可得![]() ,证明
,证明![]() ,得出
,得出![]() ,利用角的和差关系可推出
,利用角的和差关系可推出![]() ,再证明
,再证明![]() ,得出
,得出![]() ,即可得出结论.
,即可得出结论.
解:(1)∵![]()
∴![]()
∴![]()
在![]() 中根据三角形三边关系可得出:
中根据三角形三边关系可得出:
![]() ,即
,即![]()
∴![]()
故答案为:![]() ;
;
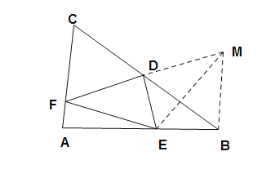
(2)延长FD至M,使DF=DM,连接BM,EM,
同(1)可得出![]() ,
,
∵![]()
∴![]()
在![]() 中,
中,![]()
∴![]() ;
;
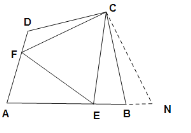
(3)![]() ,理由如下:
,理由如下:
延长AB至N,使BN=DF,连接CN,
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() (SAS)
(SAS)
∴![]()
∴![]()
∴![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
月份 销售额 人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 6 | 9 | 10 | 8 | 8 |
乙 | 5 | 7 | 8 | 9 | 9 |
丙 | 5 | 9 | 10 | 5 | 11 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 众数(万元) | 中位数(万元) | 方差 |
甲 | 8 | 8 | 1.76 | |
乙 | 7.6 | 8 | 2.24 | |
丙 | 8 | 5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.