题目内容
【题目】如图,距沿海某城市A正南220千米的B处,有一台风中心,其最大风力为12级,每远离台风中心20千米,风力就减弱1级,该中心正以每小时15千米的速度沿北偏东30°的BC方向移动,且风力不变,若城市A所受风力达到或超过4级,则称为受台风影响.
(1)A城市是否会受台风影响?为什么?
(2)若会,将持续多长时间?
(3)该城市受台风影响的最大风力为几级?
【答案】(1)会受到影响,距台风中心160千米就会受到影响.而A城到台风路线BC距离为110千米; (2) 持续4![]() 小时; (3)最大风力6.5级.
小时; (3)最大风力6.5级.
【解析】
(1)求是否会受到台风的影响,就是求A到BC的距离是否大于台风影响范围的半径,如果大于,则不受影响,反之则受影响.如果过A作AD⊥BC于D,AD就是所求的线段,直角三角形ABD中,有∠ABD的度数,有AB的长,AD就不难求出了,因此可以求出答案.
(2)受台风影响时,台风中心移动的距离,应该是A为圆心,台风影响范围的半径为半径,所得圆截得的BC上的线段的长即EF得长,可通过在直角三角形AED和AFD中,根据勾股定理求得,有了路程,有了速度,即可求出时间.
(3)风力最大时,台风中心应该位于D点,然后根据题目给出的条件判断出时几级风.
解:(1) 该城市会受到这次台风的影响.
理由是:如图,过A作AD⊥BC于D.
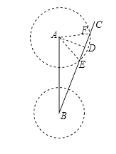
在Rt△ABD中,
∵∠ABD=30°,AB=220,
∴![]() ,
,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为20×(12-4)=160.
∵110<160,
∴该城市会受到这次台风的影响.
(2) 如上图,以A为圆心,160为半径作⊙A交BC于E、F,
则AE=AF=160,
∴台风影响该市持续的路程为:![]() ,
,
∴台风影响该市的持续时间为:t=![]() ÷15=4
÷15=4![]()
(3)∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12-(110÷20)=12-5.5=6.5(级),
故最大风力6.5级.

 阅读快车系列答案
阅读快车系列答案