题目内容
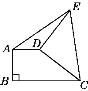
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为____________.
【答案】5
【解析】
过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,由旋转的性质可知△CDF≌△EDG,从而有CF=EG,由△ADE的面积可求EG,得出CF的长,由矩形的性质得BF=AD,根据BC=BF+CF求解.
解:过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,

由旋转的性质可知CD=ED,
∵∠EDG+∠CDG=∠CDG+∠FDC=90°,
∴∠EDG=∠FDC,又∠DFC=∠G=90°,
∴△CDF≌△EDG,∴CF=EG,
∵S△ADE=![]() AD×EG=3,AD=2,
AD×EG=3,AD=2,
∴EG=3,则CF=EG=3,
依题意得四边形ABFD为矩形,∴BF=AD=2,
∴BC=BF+CF=2+3=5.
故答案为:5.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
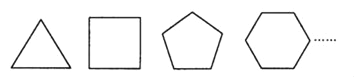
(1)请根据下列图形,填写表中空格:
正多边形边数 | 3 | 4 | 5 | 6 | … |
正多边形每个内角的度数 | … |
(2)如图,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.