题目内容
如图,已知梯形ABCD中,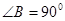 ,AD//BC,沿着CE翻折,点D与点B重合,AD=2,AB=4,则
,AD//BC,沿着CE翻折,点D与点B重合,AD=2,AB=4,则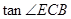 = ▲ ,CD= ▲ .
= ▲ ,CD= ▲ .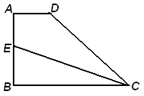
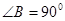 ,AD//BC,沿着CE翻折,点D与点B重合,AD=2,AB=4,则
,AD//BC,沿着CE翻折,点D与点B重合,AD=2,AB=4,则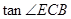 = ▲ ,CD= ▲ .
= ▲ ,CD= ▲ .
 ,5
,5过点D作DF⊥BC于点F,连接ED,设EB=x,BC=y,在RT△AED中,利用勾股定理可求出EB的长度,在RT△DFC中,利用勾股定理可求出BC的长度,继而可得出答案.
解:过点D作DF⊥BC于点F,连接ED,

设EB=x,则AE=4-x,
在RT△AED中,ED2=AE2+AD2,即x2=(4-x)2+22,
解得:x= ,即EB=ED=
,即EB=ED= ,AE=4-
,AE=4- =
= ,
,
设BC=y,则FC=y-2,CD=y,
在RT△DFC中,DF2+FC2=DC2,即42+(y-2)2=y2,
解得:y=5,即BC=CD=5,
tan∠ECB= .
.
故答案为: ,5.
,5.
解:过点D作DF⊥BC于点F,连接ED,

设EB=x,则AE=4-x,
在RT△AED中,ED2=AE2+AD2,即x2=(4-x)2+22,
解得:x=
 ,即EB=ED=
,即EB=ED= ,AE=4-
,AE=4- =
= ,
,设BC=y,则FC=y-2,CD=y,
在RT△DFC中,DF2+FC2=DC2,即42+(y-2)2=y2,
解得:y=5,即BC=CD=5,
tan∠ECB=
 .
.故答案为:
 ,5.
,5.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则图中阴影部分的面积是___________。
,则图中阴影部分的面积是___________。
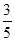 ,sinA′=
,sinA′=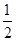 .
.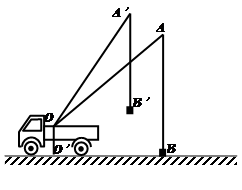

 ,则tanA的值为
,则tanA的值为


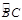 和弦AC的长. (弧长计算结果保留
和弦AC的长. (弧长计算结果保留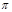 ,弦长精确到0.01)
,弦长精确到0.01)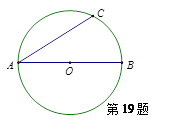
 ,则锐角α的度数是( )
,则锐角α的度数是( ) ,求∠DCB的度数.
,求∠DCB的度数. 
