题目内容
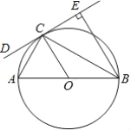
【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.
(1)求证:BC平分∠ABE;
(2)若∠A=60°OA=4,求CE的长.
【答案】(1)证明见解析;(2)CE=2![]() .
.
【解析】
(1)由∠ACB是直角,BE⊥CD,且OC=OB,可证BC平分∠ABE;
(2)∠A=60°,可得∠ABC=∠CBE=30°,OA=4,所以,BC=4![]() ,所以在直角三角形CBE中,CE=
,所以在直角三角形CBE中,CE=![]() BC=2
BC=2![]() .
.
(1)∵CD是⊙O的切线,∴OC⊥DE,
而BE⊥DE,∴OC∥BE,∴∠OCB=∠CBE,
而OB=OC,∴∠OCB=∠CBO,∴∠OBC=∠CBE,即BC平分∠ABE;
(2)∵AB为直径,∴∠ACB=90°,∵sinA=![]() ,∴BC=8sin60°=4
,∴BC=8sin60°=4![]() ,
,
∵∠OBC=∠CBE=30°,在Rt△CBE中,CE=![]() BC=2
BC=2![]() .
.

练习册系列答案
相关题目