题目内容
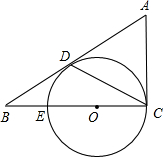
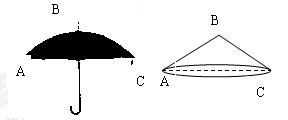
如图,有一块圆形铁皮,BC是⊙O的直径,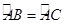 ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分).
(1)当⊙O的半径为2时,求这个扇形(阴影部分)的面积(结果保留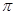 );
);
(2)当⊙O的半径为R(R>0)时,在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形
围成一个圆锥?请说明理由.
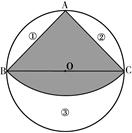
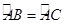 ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分).(1)当⊙O的半径为2时,求这个扇形(阴影部分)的面积(结果保留
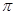 );
);(2)当⊙O的半径为R(R>0)时,在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形
围成一个圆锥?请说明理由.

连接AO并延长交扇形、圆于点E、F
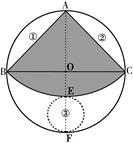
∵BC是⊙O的直径,∴∠BAC="90°"
 ∵
∵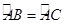 ∴AB=AC,
∴AB=AC,
∵AO=BO ∴AF⊥BC
(1)当⊙O的半径为2时:AC=AB=2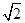
∴S阴影=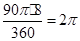 ;
;
(2)当⊙O的半径为R(R>0)时:AC=AB=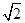 R
R
阴影部分扇形的弧长为: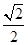 πR
πR
EF=2R-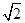 R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-
R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-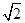 )πR
)πR
∵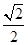 πR>(2-
πR>(2-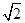 )πR
)πR
∴不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.

∵BC是⊙O的直径,∴∠BAC="90°"
 ∵
∵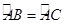 ∴AB=AC,
∴AB=AC, ∵AO=BO ∴AF⊥BC
(1)当⊙O的半径为2时:AC=AB=2
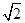
∴S阴影=
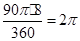 ;
; (2)当⊙O的半径为R(R>0)时:AC=AB=
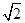 R
R 阴影部分扇形的弧长为:
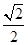 πR
πR EF=2R-
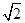 R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-
R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-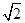 )πR
)πR ∵
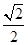 πR>(2-
πR>(2-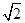 )πR
)πR∴不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
(1)先由圆的性质求得阴影部分扇形的半径,由直径所对的圆周角是90°可知圆心角的度数,可求得阴影部分的面积;
(2)先分别用R表示出阴影部分扇形的弧长,即所要围成的圆锥的底面周长为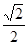 Rπ,以EF为直径作圆,是剩余材料中所作的最大的圆,求出其周长为(2-
Rπ,以EF为直径作圆,是剩余材料中所作的最大的圆,求出其周长为(2-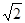 )Rπ,比较大小可知不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
)Rπ,比较大小可知不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
(2)先分别用R表示出阴影部分扇形的弧长,即所要围成的圆锥的底面周长为
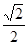 Rπ,以EF为直径作圆,是剩余材料中所作的最大的圆,求出其周长为(2-
Rπ,以EF为直径作圆,是剩余材料中所作的最大的圆,求出其周长为(2-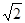 )Rπ,比较大小可知不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
)Rπ,比较大小可知不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.请你根据题意,在图上画出圆心O运动路径的示意图;圆心O运动的路程是 ▲ .
,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.请你根据题意,在图上画出圆心O运动路径的示意图;圆心O运动的路程是 ▲ .
 是⊙
是⊙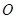 外一点,
外一点,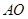 的延长线交⊙
的延长线交⊙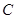 和点
和点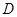 ,点
,点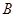 在圆上,且
在圆上,且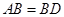 ,∠
,∠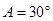 .
.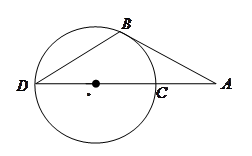
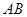 是⊙
是⊙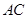 的长.
的长. 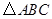 中,
中,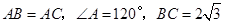 ,
,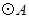 与
与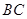 相切于点
相切于点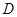 ,且交
,且交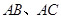 于
于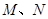 两点,则图中阴影部分的面积是 (结果保留根号和
两点,则图中阴影部分的面积是 (结果保留根号和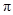 的形式).
的形式).
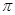
 内接于⊙
内接于⊙ ,
, 为线段
为线段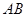 的中点,延长
的中点,延长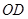 交⊙
交⊙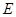 ,连结
,连结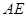 ,
,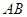 ,则下列五个结论:①
,则下列五个结论:①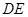 ,②
,②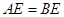 ,③
,③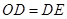 ,④
,④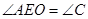 ,⑤
,⑤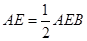 ,正确结论的个数有( )
,正确结论的个数有( )
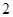 个
个 个
个 个
个 个
个