题目内容
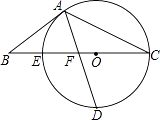
【题目】(10分)如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)试说明OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由.

【答案】详见解析.
【解析】
试题分析:(1)根据正方形的性质对角线垂直且平分,得到OB=OA,又因为AM⊥BE,所以∠MEA+∠MAE=90°=∠AFO+∠MAE,从而求证出Rt△BOE≌Rt△AOF,得到OE=OF.(2)根据第一步得到的结果以及正方形的性质得到OB=OA,再根据已知条件求证出Rt△BOE≌Rt△AOF,得到OE=OF.
试题解析:(1)证明:∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
∴Rt△BOE≌Rt△AOF.
∴OE=OF.
解:OE=OF成立.
证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
∴Rt△BOE≌Rt△AOF.
∴OE=OF.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】2013年是一个让人记忆犹新的年份,雾霾天气持续笼罩我国大部分地区,口罩市场出现热销,某旗舰网店用8000元购进甲、乙两种型号的口罩,销售完后共获利2800元,进价和售价如下表:
品名 价格 | 甲型口罩 | 乙型口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种型号口罩各多少袋?
(2)该网店第二次以原价购进甲、乙两种型号口罩,购进乙种型号口罩袋数不变,而购进甲种型号口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种型号的口罩都售完,要使第二次销售活动获利不少于3680元,乙种型号的口罩最低售价为每袋多少元?
【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表:
选手 | 选拔成绩/环 | 中位数 | 平均数 | |||||
甲 | 10 | 9 | 8 | 8 | 10 | 9 | ||
乙 | 10 | 10 | 8 | 10 | 7 | 9 | ||
(1)把表中所空各项数据填写完整;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1),(2)计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.