题目内容
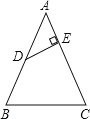
【题目】如图1,是一个长为![]() ,宽为
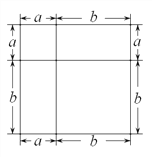
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
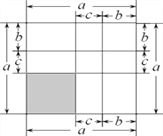
(1)你认为图2中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法求图2中阴影部分的面积.
方法1 ;方法2 ;
(3)仔细观察图2,写出![]() 三个代数式之间的等量关系.
三个代数式之间的等量关系.
(4)若![]() ,求
,求![]() 的值.
的值.

【答案】(1)a-b ;(2)法一 a2-2ab+b2 法二 (a+b)2 -4ab;(3)(a-b)2= (a+b)2-4ab;(4)-7,+7.
【解析】
(1)直接写出边长:长边一短边=a-b;
(2)直接根据边长的平方计算面积或根据面积差计算面积;
(3)根据图形利用面积可得结论;
(4)结合(3)的结论和完全平方公式,先计算xy的值,再计算(x-y)2的值,最后开方可得结论.
(1)图2中的阴影部分的正方形的边长等于a-b;
(2)方法一:S阴影=S正方形-4S长方形=(a+b)2-4ab=(a-b)2;
方法二:∵分成的四块小长方形形状和大小都一样,
∴每一个小长方形的长为a,宽为b,
∴阴影部分的正方形的边长为(a-b),
∴S阴影=(a-b)2,
(3)由图2得:(a+b)2-4ab=(a-b)2;
(4)∵(x+y)2=x2+2xy+y2,
∵x+y=1,x2+y2=25,
∴1=25+2xy,
xy=-12,
∵(x+y)2-4xy=(x-y)2,
∴(x-y)2=1-4×(-12)=49,
∴x-y=±7.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(注:方差公式 ![]() .)
.)
(1)完成表中填空①;②;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩的方差为 ![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.