题目内容
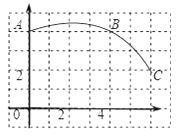
【题目】如图,直角三角形的斜边![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 与原点重合,点
与原点重合,点![]() 的坐标是
的坐标是![]() ,且
,且![]() ,若将
,若将![]() 绕着点
绕着点![]() 旋转后30°,点
旋转后30°,点![]() 和
和![]() 点分别落在点
点分别落在点![]() 和点
和点![]() 处,那么直线
处,那么直线![]() 的解析式是__________.
的解析式是__________.

【答案】![]() 和
和![]()
【解析】
先求出E、F点的坐标,再利用待定系数法即可求得.
解:∵点B的坐标是(0,4),且∠A=30°.
∴AB=4,
∵在Rt△ABC中,∠BAC=30°,
∴BC=![]() AB=2,
AB=2,
∴AC=![]() ,
,
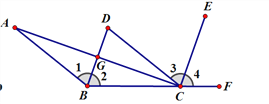
当逆时针旋转30°后,如图所示,

∵旋转
∴EF=BC=2,AF=AC=![]()
点E(-2,![]() ),F(0,
),F(0,![]() ),
),
∴直线EF的解析式是 y=![]() ;
;
当逆时针旋转30°后,如图所示,过点E、F分别作EG⊥x轴,FH⊥x轴,垂足为点G、H,

∵旋转
∴AE=AB=4,AF=AC=![]() ,∠EAF=∠BAC=30°,
,∠EAF=∠BAC=30°,
∵EG∥y轴,
∴∠AEG=∠BAC=30°,
∵在Rt△EAG中,∠AEG=30°,
∴AG=![]() AE=2,
AE=2,
∴EG=![]() ,
,
∴点E(2,![]() ),
),
∵∠EAF=∠BAC=30°,
∴∠FAH=90°-∠EAF-∠BAC=30°,
∵在Rt△FAH中,∠FAH=30°,
∴FH=![]() AF=
AF=![]() ,
,
∴AH=![]() ,
,
∴点F(3,![]() ),
),
设直线EF的解析式为y=kx+b,
∴ ,解得
,解得 ,
,
∴直线EF的解析式为y=![]() x+4
x+4![]() ,
,
故答案为:y=![]() 或y=
或y=![]() x+4
x+4![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目