题目内容
如图，在Rt△ABC中，CD是斜边AB上的高，AE平分∠CAB且交CD于点G，EF⊥AB于点F，则下列结论中不正确的是（ ）
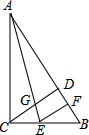
| A．∠ACD=∠B | B．CE=EF | C．AC=AF | D．CG=GD |
A、∵CD⊥AB，
∴∠ADC=∠ACB=90°，
∴∠CAD+∠ACD=90°，∠B+∠CAB=90°，
∴∠ACD=∠B，正确，故本选项错误；
B、∵AE平分∠CAB，∠ACB=90°，EF⊥AB，
∴CE=EF，
∵AE平分∠CAB，
∴∠CAE=∠BAE，
∵∠B=∠ACD，
∴∠ACD+∠CAE=∠B+∠BAE，
即∠CHE=∠CEH，
∴CE=EF，正确，故本选项错误；
C、在Rt△ACE和Rt△AFE中，AE=AE，CE=EF，由勾股定理得：AC=AF，正确，故本选项错误；
D、CG=EF＞GD，错误，故本选项正确．
故选D．
∴∠ADC=∠ACB=90°，
∴∠CAD+∠ACD=90°，∠B+∠CAB=90°，
∴∠ACD=∠B，正确，故本选项错误；
B、∵AE平分∠CAB，∠ACB=90°，EF⊥AB，
∴CE=EF，
∵AE平分∠CAB，
∴∠CAE=∠BAE，
∵∠B=∠ACD，
∴∠ACD+∠CAE=∠B+∠BAE，
即∠CHE=∠CEH，
∴CE=EF，正确，故本选项错误；
C、在Rt△ACE和Rt△AFE中，AE=AE，CE=EF，由勾股定理得：AC=AF，正确，故本选项错误；
D、CG=EF＞GD，错误，故本选项正确．
故选D．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
