题目内容
如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E是⊙O上一点,D是AM上一点,连接DE并延长交BN于点C,且OD∥BE,OF∥BN.
(1)求证:DE与⊙O相切;
(2)求证:OF=
CD.

(1)求证:DE与⊙O相切;
(2)求证:OF=
| 1 |
| 2 |

证明:(1)连接OE,
∵AM与圆O相切,
∴AM⊥OA,即∠OAD=90°,
∵OD∥BE,
∴∠AOD=∠ABE,∠EOD=∠OEB,
∵OB=OE,
∴∠ABE=∠OEB,
∴∠AOD=∠EOD,
在△AOD和△EOD中,
,
∴△AOD≌△EOD(SAS),
∴∠OED=∠OAD=90°,
则DE为圆O的切线;
(2)在Rt△BCO和Rt△ECO中,
,
∴Rt△BCO≌Rt△ECO,
∴∠BOC=∠EOC,
∵∠AOD=∠EOD,
∴∠DOC=∠EOD+∠EOC=
×180°=90°,
∵AM、BN为圆O的切线,
∴AM⊥AB,BN⊥AB,
∴AM∥BN,
∵OF∥BN,
∴AM∥OF∥BN,
又O为AB的中点,
∴F为CD的中点,
则OF=
CD.
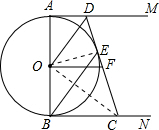
∵AM与圆O相切,
∴AM⊥OA,即∠OAD=90°,
∵OD∥BE,
∴∠AOD=∠ABE,∠EOD=∠OEB,
∵OB=OE,
∴∠ABE=∠OEB,
∴∠AOD=∠EOD,
在△AOD和△EOD中,
|
∴△AOD≌△EOD(SAS),
∴∠OED=∠OAD=90°,
则DE为圆O的切线;
(2)在Rt△BCO和Rt△ECO中,
|
∴Rt△BCO≌Rt△ECO,
∴∠BOC=∠EOC,
∵∠AOD=∠EOD,
∴∠DOC=∠EOD+∠EOC=
| 1 |
| 2 |
∵AM、BN为圆O的切线,
∴AM⊥AB,BN⊥AB,
∴AM∥BN,
∵OF∥BN,
∴AM∥OF∥BN,
又O为AB的中点,
∴F为CD的中点,
则OF=
| 1 |
| 2 |


练习册系列答案
相关题目




 点D,且∠D=∠BAC.
点D,且∠D=∠BAC.