Question

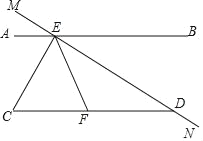
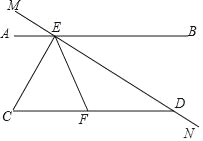
【题目】如图，∠AEM＝30°，CE⊥MN，垂足为点E，∠CDN＝150°，EC平分∠AEF．

（1）求∠C的度数；

（2）求证：∠FDE＝∠FED．

Answer 1

【答案】(1) ∠C＝60°;(2)见解析.

【解析】

（1）由垂直可得∠AEC＝60°，又由∠CDE和∠CDN互补可得∠CDE＝30°，则AB∥CD，根据两直线平行同位角相等则∠C＝60°.（2）由角平分线可得∠AEC＝∠CEF，再由平角180°，求出∠FED＝30°，等量代换得∠FED＝∠EDF．

证明：（1）∵CE⊥MN，（已知），

∴∠MEC＝90°，（ 垂直定义），

∵∠AEM＝30°，

∴∠AEC＝∠MEC﹣∠AEM＝90°﹣30°＝60°，

∵∠CDE+∠CDN＝180°（平角的定义），

∠CDN＝150°，

∴∠CDE＝180°﹣∠CDN＝180°﹣150°＝30°，

∴∠CDE＝∠AEM（等量代换），

∴AB∥CD（同位角相等，两直线平行），

∴∠C＝∠AEC（两直线平行，内错角相等），

即∠C＝60°，

（2）∵EC平分∠AEF．（已知），

∴∠AEC＝∠CEF（角平分线的定义），

∠FED＝180°﹣∠AEC﹣∠CEF﹣∠AEM＝180°﹣60°﹣60°﹣30°＝30°，

∴∠FED＝∠EDF．