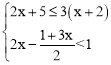题目内容
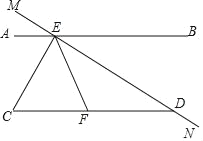
【题目】问题情境1:如图1,AB∥CD,P是ABCD内部一点,P在BD的右侧,探究∠B,∠P,∠D之间的关系?
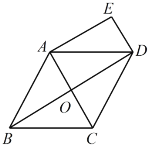
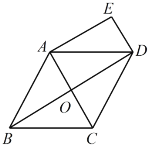
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠B,∠P,∠D之间满足 关系.(直接写出结论)

问题情境2
如图3,AB∥CD,P是AB,CD内部一点,P在BD的左侧,可得∠B,∠P,∠D之间满足 关系.(直接写出结论)
问题迁移:请合理的利用上面的结论解决以下问题:
已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F
(1)如图4,若∠E=80°,求∠BFD的度数;
(2)如图5中,∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,设∠E=m°,用含有n,m°的代数式直接写出∠M= .
∠CDF,设∠E=m°,用含有n,m°的代数式直接写出∠M= .
【答案】问题情境1:∠B+∠BPD+∠D=360°,∠P=∠B+∠D;(1)140°;(2)![]() ∠E+∠M=60°(3)
∠E+∠M=60°(3)![]()
【解析】
问题情境1:过点P作PE∥AB,根据平行线的性质,得到∠B+∠BPE=180°,∠D+∠DPE=180°,进而得出:∠B+∠P+∠D=360°;
问题情境2:过点P作EP∥AB,再由平行线的性质即可得出结论;
②,③根据①中的方法可得出结论;
问题迁移:
(1)如图4,根据角平分线定义得:∠EBF=![]() ∠ABE,∠EDF=
∠ABE,∠EDF=![]() ∠CDE,由问题情境1得:∠ABE+∠E+∠CDE=360°,再根据四边形的内角和可得结论;
∠CDE,由问题情境1得:∠ABE+∠E+∠CDE=360°,再根据四边形的内角和可得结论;
(2)设∠ABM=x,∠CDM=y,则∠FBM=2x,∠EBF=3x,∠FDM=2y,∠EDF=3y,根据问题情境和四边形内角和得等式可得结论;
(3)同(2)将3倍换为n倍,同理可得结论.
问题情境1:
如图2,∠B+∠BPD+∠D=360°,理由是:
过P作PE∥AB,

∵AB∥CD,PE∥AB,
∴AB∥PE∥CD,
∴∠B+∠BPE=180°,∠D+∠DPE=180°,
∴∠B+∠BPE+∠D+∠DPE=360°,
即∠B+∠BPD+∠D=360°,
故答案为:∠B+∠P+∠D=360°;
问题情境2
如图3,∠P=∠B+∠D,理由是:
过点P作EP∥AB,

∵AB∥CD,
∴AB∥CD∥EP,
∴∠B=∠BPE,∠D=∠DPE,
∴∠BPD=∠B+∠D,
即∠P=∠B+∠D;
故答案为:∠P=∠B+∠D;
问题迁移:
(1)如图4,∵BF、DF分别是∠ABE和∠CDE的平分线,
∴∠EBF=![]() ∠ABE,∠EDF=
∠ABE,∠EDF=![]() ∠CDE,
∠CDE,
由问题情境1得:∠ABE+∠E+∠CDE=360°,
∵∠E=80°,
∴∠ABE+∠CDE=280°,
∴∠EBF+∠EDF=140°,
∴∠BFD=360°﹣80°﹣140°=140°;
(2)如图5,![]() ∠E+∠M=60°,理由是:
∠E+∠M=60°,理由是:
∵设∠ABM=x,∠CDM=y,则∠FBM=2x,∠EBF=3x,∠FDM=2y,∠EDF=3y,
由问题情境1得:∠ABE+∠E+∠CDE=360°,
∴6x+6y+∠E=360°,
![]() ∠E=60﹣x﹣y,
∠E=60﹣x﹣y,
∵∠M+∠EBM+∠E+∠EDM=360°,
∴6x+6y+∠E=∠M+5x+5y+∠E,
∴∠M=x+y,
∴![]() ∠E+∠M=60°;
∠E+∠M=60°;
(3)如图5,∵设∠ABM=x,∠CDM=y,则∠FBM=(n﹣1)x,∠EBF=nx,∠FDM=(n﹣1)y,∠EDF=ny,
由问题情境1得:∠ABE+∠E+∠CDE=360°,
∴2nx+2ny+∠E=360°,
∴x+y=![]() ,
,
∵∠M+∠EBM+∠E+∠EDM=360°,
∴2nx+2ny+∠E=∠M+(2n﹣1)x+(2n﹣1)y+∠E,
∴∠M=![]() ;
;
故答案为:∠M=![]() .
.

 优等生题库系列答案
优等生题库系列答案