题目内容
【题目】如图,四边形ABCD中,AD∥BC,∠BDC=90°,BD=CD,DM是BC边上的中线,过点C作CE⊥AB,垂足为E,CE交线段BD于点F,交DM于点N,连接AF.
(1)求证:∠DCN=∠DBA;
(2)直接写出线段AF、AB和CF之间的数量关系;
(3)当E恰好为AB中点时,∠BAD=______度.

【答案】(1)证明见解析;(2)AF+AB=CF;(3)105.
【解析】
(1)根据垂直的定义得到∠FEB=∠BDC=90°,根据对顶角相等得到∠DFC=∠EFB,于是得到∠DCN=∠DBA;
(2)根据等腰直角三角形的性质得到CM=BM,DM⊥BC,求得∠DMC=∠DMB=90°,根据平行线的性质得到∠MDA=90°,得到∠ADB=∠NDC=45°,根据全等三角形的性质得到AB=CN,DA=DN,AF=NF,于是得到结论;
(3)连接AC,过A作AH⊥BC于H,由矩形的性质得到DM=AH,求得AH=![]() BC,根据线段垂直平分线的性质得到AC=BC,求得AH=
BC,根据线段垂直平分线的性质得到AC=BC,求得AH=![]() AC,得到∠ACH=30°,根据平行线的性质得到结论.
AC,得到∠ACH=30°,根据平行线的性质得到结论.
解:(1)∵CE⊥AB,
∴∠FEB=∠BDC=90°,
∵∠DFC=∠EFB,
∴∠DCN=∠DBA,
(2)∵BD=CD,∠BDC=90°
∴△BDC是等腰直角三角形,
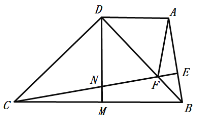
又∵DM为BC边中线,
∴CM=BM,DM⊥BC,
∴∠DMC=∠DMB=90°,
又∵AD∥BC,
∴∠MDA=90°,
又∵∠BDC=90°,
∴∠ADB=∠NDC=45°,
∴△ADB≌△NDC(ASA),
∴AB=CN,DA=DN,
∴∠ADF=∠NDF,
∴△ADF≌△NDF(SAS),
∴AF=NF,
∴CF=CN+NF=AB+AF,
∴AF+AB=CF;
(3)连接AC,过A作AH⊥BC于H,
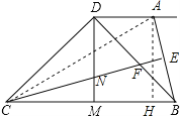
∴四边形ADMH是矩形,
∴DM=AH,
∴AH=![]() BC,
BC,
∵E恰好为AB中点,CE⊥AB,
∴AC=BC,
∴AH=![]() AC,
AC,
∴∠ACH=30°,
∴∠ABC=∠CAB=![]() =75°,
=75°,
∵AD∥BC,
∴∠DAC=∠ACB=30°,
∴∠DAB=105°,
故答案为:105.

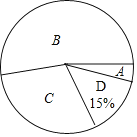
【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.