题目内容
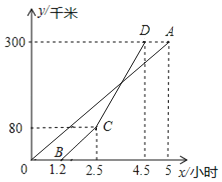
【题目】甲、乙两地相距300千米，一辆货车和一辆轿车分别从甲地开往乙地
轿车的平均速度大于货车的平均速度
，如图，线段OA、折线BCD分别表示两车离甲地的距离
单位：千米与时间
单位：小时之间的函数关系．
线段OA与折线BCD中，______表示货车离甲地的距离y与时间x之间的函数关系．
求线段CD的函数关系式；
货车出发多长时间两车相遇？
【答案】（1）线段OA表示货车货车离甲地的距离y与时间x之间的函数关系；（2）
；（3）货车出发
小时两车相遇．
【解析】
(1)根据题意可以分别求得两个图象中相应函数对应的速度，从而可以解答本题；
(2)设CD段的函数解析式为y=kx+b，将C(2.5,80)，D(4.5,300)两点的坐标代入，运用待定系数法即可求解；
(3)根据题意可以求得OA对应的函数解析式，从而可以解答本题．
线段OA表示货车货车离甲地的距离y与时间x之间的函数关系，
理由：
千米
时
，
，
，轿车的平均速度大于货车的平均速度，
线段OA表示货车离甲地的距离y与时间x之间的函数关系，
故答案为：OA；
设CD段函数解析式为
，
，
在其图象上，
，解得
，
段函数解析式：
；
设线段OA对应的函数解析式为
，
，得
，
即线段OA对应的函数解析式为
，
，解得
，
即货车出发小时两车相遇．
【题目】某公司根据市场计划调整投资策略，对A、B两种产品进行市场调查，收集数据如下表：
项目 产品 | 年固定成本 （单位：万元） | 每件成本 （单位：万元） | 每件产品销售价 （万元） | 每年最多可生产的件数 |
A | 20 | m | 10 | 200 |
B | 40 | 8 | 18 | 120 |
其中，m是待定系数，其值是由生产A的材料的市场价格决定的，变化范围是6≤m＜8，销售B产品时需缴纳
x2万元的关税．其中，x为生产产品的件数．假定所有产品都能在当年售出，设生产A，B两种产品的年利润分别为y1、y2（万元）．
（1）写出y1、y2与x之间的函数关系式，注明其自变量x的取值范围．
（2）请你通过计算比较，该公司生产哪一种产品可使最大年利润更大？
