Question

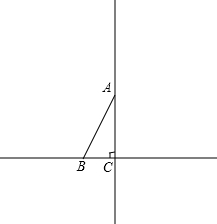
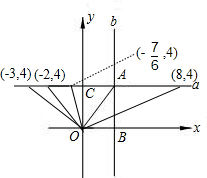
如图，在平面直角坐标系xoy中，分别平行x、y轴的两直线a、b相交于点A（3，4）．连接OA，若在直线a上存在点P，使△AOP是等腰三角形．那么所有满足条件的点P的坐标是______．

Answer 1

∵A（3，4）
∴OB=3，AB=4
∴0A=

OB2+AB2

=5
∴当OA为等腰三角形一条腰，则点P的坐标是（8，4）（-2，4）（-3，4）；
当OA为底边时，
∵A（3，4），
∴直线OA的解析式为y=

4

3

x，
∴过线段OA的中点且与直线OA垂直的直线解析式为：y=-

3

4

x+

25

8

，
∴点P的坐标是（-

7

6

，4）．
故填（8，4）或（-2，4）或（-3，4）或（-

7

6

，4）．