题目内容
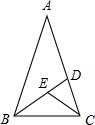
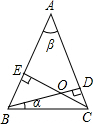
如图,在△ABC中,AB=AC,BD、CE分别是两腰上的高,且BD、CE相交于O.
(1)请你写出三类不同的正确的结论;
(2)设∠CBD=α,∠A=β,试找出α与β之间的一种关系等式,并给予适当的说明(友情提示:∠ABC=∠ACB).
(1)请你写出三类不同的正确的结论;
(2)设∠CBD=α,∠A=β,试找出α与β之间的一种关系等式,并给予适当的说明(友情提示:∠ABC=∠ACB).

(1)三类不同的正确结论是:
①△CEB≌△BDC;②∠ABD=∠ACE;③AE=AD;
(2)α与β之间的一种关系式是β=2α.
其理由是:
∵BD⊥AC,∴∠CBD+∠ACB=90°,
即α+∠ACB=90°.
∵AB=AC,
∴∠ABC=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴β+2∠ACB=180°,
即β+2(90°-α)=180°,
∴β=2α.
①△CEB≌△BDC;②∠ABD=∠ACE;③AE=AD;
(2)α与β之间的一种关系式是β=2α.
其理由是:
∵BD⊥AC,∴∠CBD+∠ACB=90°,
即α+∠ACB=90°.
∵AB=AC,
∴∠ABC=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴β+2∠ACB=180°,
即β+2(90°-α)=180°,
∴β=2α.

练习册系列答案
相关题目