ЬтФПФкШн
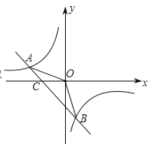
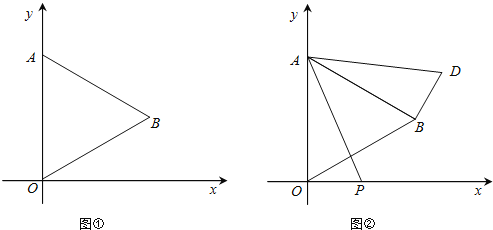
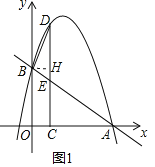
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§yЃНЉ![]() x+3ЕФЭМЯѓгыxжсНЛгкЕуAЃЌгыyжсНЛгкBЕуЃЌХзЮяЯпyЃНЉx2+bx+cОЙ§AЃЌBСНЕуЃЌдкЕквЛЯѓЯоЕФХзЮяЯпЩЯШЁвЛЕуDЃЌЙ§ЕуDзїDCЁЭxжсгкЕуCЃЌНЛжБЯпABгкЕуEЃЎ
x+3ЕФЭМЯѓгыxжсНЛгкЕуAЃЌгыyжсНЛгкBЕуЃЌХзЮяЯпyЃНЉx2+bx+cОЙ§AЃЌBСНЕуЃЌдкЕквЛЯѓЯоЕФХзЮяЯпЩЯШЁвЛЕуDЃЌЙ§ЕуDзїDCЁЭxжсгкЕуCЃЌНЛжБЯпABгкЕуEЃЎ
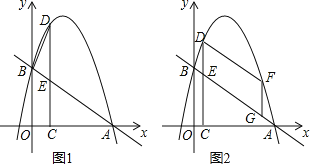
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪН
ЃЈ2ЃЉЪЧЗёДцдкЕуDЃЌЪЙЕУЁїBDEКЭЁїACEЯрЫЦЃПШєДцдкЃЌЧыЧѓГіЕуDЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
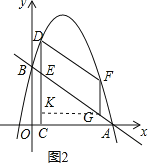
ЃЈ3ЃЉШчЭМ2ЃЌFЪЧЕквЛЯѓЯоФкХзЮяЯпЩЯЕФЖЏЕуЃЈВЛгыЕуDжиКЯЃЉЃЌЕуGЪЧЯпЖЮABЩЯЕФЖЏЕуЃЎСЌНгDFЃЌFGЃЌЕБЫФБпаЮDEGFЪЧЦНааЫФБпаЮЧвжмГЄзюДѓЪБЃЌЧыжБНгаДГіЕуGЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+![]() x+3ЃЛЃЈ2ЃЉДцдкЃЎЕуDЕФзјБъЮЊЃЈ
x+3ЃЛЃЈ2ЃЉДцдкЃЎЕуDЕФзјБъЮЊЃЈ![]() ЃЌ3ЃЉЛђЃЈ
ЃЌ3ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉGЃЈ
ЃЉЃЛЃЈ3ЃЉGЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОн![]() ЃЌЧѓГіAЃЌBЕФзјБъЃЌдйДњШыХзЮяЯпНтЮіЪНжаМДПЩЧѓЕУХзЮяЯпНтЮіЪНЃЛ
ЃЌЧѓГіAЃЌBЕФзјБъЃЌдйДњШыХзЮяЯпНтЮіЪНжаМДПЩЧѓЕУХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЁїBDEКЭЁїACEЯрЫЦЃЌвЊЗжСНжжЧщПіНјааЬжТлЃКЂйЁїBDEЁзЁїACEЃЌЧѓЕУ![]() ЃЌ
ЃЌ![]()
ЃЛЂкЁїDBEЁзЁїACEЃЌЧѓЕУ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉгЩDEGFЪЧЦНааЫФБпаЮЃЌПЩЕУDEЁЮFGЃЌDE=FGЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌИљОнЦНааЫФБпаЮжмГЄЙЋЪНПЩЕУЃКDEGFжмГЄ=
ЃЌИљОнЦНааЫФБпаЮжмГЄЙЋЪНПЩЕУЃКDEGFжмГЄ=![]() ЃЌгЩДЫПЩЧѓЕУЕуGЕФзјБъЃЎ
ЃЌгЩДЫПЩЧѓЕУЕуGЕФзјБъЃЎ
НтЃКЃЈ1ЃЉдк![]() жаЃЌСю
жаЃЌСю![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌСю
ЃЌСю![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
НЋ![]() ЃЌ
ЃЌ![]() ЗжБ№ДњШыХзЮяЯп
ЗжБ№ДњШыХзЮяЯп![]() жаЃЌЕУЃК
жаЃЌЕУЃК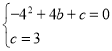 ЃЌНтЕУЃК
ЃЌНтЕУЃК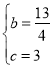 ЃЌ
ЃЌ
![]() ХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃК
ХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃК![]() ЃЎ
ЃЎ
ЃЈ2ЃЉДцдкЃЎШчЭМ1ЃЌЙ§Еу![]() зї
зї![]() гк
гк![]() ЃЌЩш
ЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]() КЭ
КЭ![]() ЯрЫЦЃЌ
ЯрЫЦЃЌ![]()
![]() Лђ
Лђ![]()
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
![]()
![]() ЃЌМДЃК
ЃЌМДЃК![]()
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]()
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
![]()
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌМДЃК
ЃЌМДЃК![]()
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЈЩс
ЃЈЩс![]() ЃЌ
ЃЌ![]() ЃЈЩс
ЃЈЩс![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
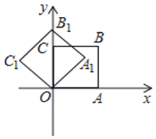
ЃЈ3ЃЉШчЭМ3ЃЌ![]() ЫФБпаЮ
ЫФБпаЮ![]() ЪЧЦНааЫФБпаЮ
ЪЧЦНааЫФБпаЮ
![]() ЃЌ
ЃЌ![]()
Щш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌМДЃК
ЃЌМДЃК![]() ЃЌ
ЃЌ![]()
![]() ЃЌМДЃК
ЃЌМДЃК![]()
Й§Еу![]() зї
зї![]() гк
гк![]() ЃЌдђ
ЃЌдђ![]()
![]()
![]()
![]() ЃЌМДЃК
ЃЌМДЃК![]()
![]() ЃЌМДЃК
ЃЌМДЃК![]()
![]() жмГЄ
жмГЄ![]()
![]() ЃЌ
ЃЌ
![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() жмГЄзюДѓжЕ
жмГЄзюДѓжЕ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ

 аЁбЇФмСІВтЪдОэЯЕСаД№АИ
аЁбЇФмСІВтЪдОэЯЕСаД№АИЁОЬтФПЁПФГжжгЭВЫзбдкЯрЭЌЬѕМўЯТЕФЗЂбПЪдбщНсЙћШчЯТБэЃК
УПХњСЃЪ§n | 5 | 10 | 70 | 130 | 310 | 700 | 1500 | 2000 | 3000 |
ЗЂбПСЃЪ§m | 4 | 9 | 60 | 116 | 282 | 639 | 1339 | 1806 | 2715 |
ЧыгУЦЕТЪЙРМЦИХТЪЕФЗНЗЈРДЙРМЦетХњгЭВЫзбдкЯрЭЌЬѕМўЯТЕФЗЂбПИХТЪЪЧ_______ЃЈОЋШЗЕН0.01ЃЉ.