Question

【题目】初2019级即将迎来中考，很多家长都在为孩子准备营养午餐．一家快餐店看准了商机，在5月5号推出了A，B，C三种营养套餐．套餐C单价比套餐A贵5元，三种套餐的单价均为整数，其中A套餐比C套餐少卖12份，B套餐比C套餐少卖6份，且C套餐当天卖出的数量大于26且不超过32，当天总销售量为偶数且当天销售额达到了1830元，商家发现C套餐很受欢迎，因此在6号加推出了C套餐升级版D套餐，四种套餐同时售卖，A套餐比5号销售量减少，C套餐比5号销售量增加，且A减少的份数比C套餐增加的份数多5份，B套餐销售量不变，由于商家人手限制，两天的总销售量相同，则其他套餐单价不变的情况下，D套餐至少比C套餐费贵______时，才能使6号销售额达到1950元．

Answer 1

【答案】9元

【解析】

设5号时，A套餐单价为x元，销售量为y份，B套餐单价为z元，6号时，D套餐比C套餐贵a元时，才能使6号销售额达到1950元．则5号时，C套餐单价为（x+5）元，B套餐销量为（y+6）份，C套餐销售（y+12）份；先根据两天的总销售量相同，可得D套餐6号的销量为5份，根据C套餐当天卖出的数量大于26且不超过32，列式26＜y≤32，根据当天总销售量为偶数且当天销售额达到了1830元，列两式：y+y+6+y+12=3y+18，是偶数，再根据销售额达到了1830元，再列一等式，最后再根据6号销售额达到1950元．列等式，综合解出即可．

解：设5号时，A套餐单价为x元，销售量为y份，B套餐单价为z元，6号时，D套餐比C套餐贵a元时，才能使6号销售额达到1950元．则5号时，C套餐单价为（x+5）元，B套餐销量为（y+6）份，C套餐销售（y+12）份；

∵两天的总销售量相同，

∴D套餐6号的销量为5份，

由题意得：，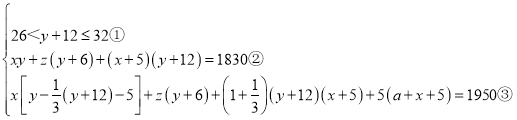

由①得：14＜y≤20，

∵y是整数，

∴y=15，16，17，18，19，20，

5号时销量为偶数，即y+y+6+y+12=3x+18，

∴符合条件的y值为16，18，20，

由②得：把y=16代入，16x+22z+28（x+5）=1830，

44x+22z=1690，

2x+z=，方程无整数解，不符合题意，

把y=18代入，18x+24z+30（x+5）=1830，

48x+24z=1680④，

把x=20代入，20x+26z+32（x+5）=1830，

52x+26z=1670，

方程无整数解，不符合题意，

∴y=18，

把y=18代入③中得：x（18-10-5）+24z++5（a+x+5）=1950，

5a+48x+24z=1725，

5a=1725-1680=45，

a=9，

故答案为：9元．