题目内容
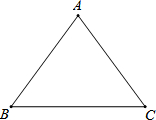（2013•上海）如图，在△ABC中，AB=AC，BC=8，tanC=| 3 |
| 2 |
| 15 |
| 4 |
| 15 |
| 4 |
分析：首先根据已知得出△ABC的高以及B′E的长，利用勾股定理求出BD即可．
解答：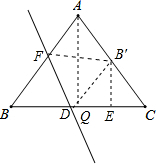
解：过点A作AQ⊥BC于点Q，
∵AB=AC，BC=8，tanC=
，
∴
=
，QC=BQ=4，
∴AQ=6，
∵将△ABC沿直线l翻折后，点B落在边AC的中点处，
过B′点作B′E⊥BC于点E，
∴B′E=
AQ=3，
∴
=
，
∴EC=2，
设BD=x，则B′D=x，
∴DE=8-x-2=6-x，
∴x2=（6-x）2+32，
解得：x=
，
直线l与边BC交于点D，那么BD的长为：
．
故答案为：
．
解：过点A作AQ⊥BC于点Q，∵AB=AC，BC=8，tanC=
| 3 |
| 2 |
∴
| AQ |
| QC |
| 3 |
| 2 |
∴AQ=6，
∵将△ABC沿直线l翻折后，点B落在边AC的中点处，
过B′点作B′E⊥BC于点E，
∴B′E=
| 1 |
| 2 |
∴
| B′E |
| EC |
| 3 |
| 2 |
∴EC=2，
设BD=x，则B′D=x，
∴DE=8-x-2=6-x，
∴x2=（6-x）2+32，
解得：x=
| 15 |
| 4 |
直线l与边BC交于点D，那么BD的长为：
| 15 |
| 4 |
故答案为：
| 15 |
| 4 |
点评：此题主要考查了翻折变换的性质以及勾股定理和锐角三角函数关系，根据已知表示出DE的长是解题关键．
练习册系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
（2013•上海）如图，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，DE∥BC，EF∥AB，且AD：DB=3：5，那么CF：CB等于（ ）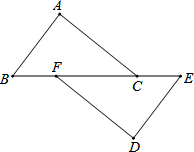
（2013•上海）如图，在△ABC和△DEF中，点B、F、C、E在同一直线上，BF=CE，AC∥DF，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是
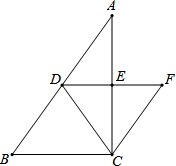（2013•上海）如图，在△ABC中，∠ACB=90°，∠B＞∠A，点D为边AB的中点，DE∥BC交AC于点E，CF∥AB交DE的延长线于点F．
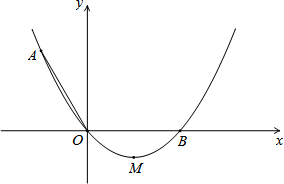（2013•上海）如图，在平面直角坐标系xOy中，顶点为M的抛物线y=ax2+bx（a＞0），经过点A和x轴正半轴上的点B，AO=OB=2，∠AOB=120°．