题目内容
【题目】如图,抛物线![]() :
:![]() 与
与![]() :
:![]() 相交于点
相交于点![]() 、
、![]() ,
,![]() 与
与![]() 分别交
分别交![]() 轴于点
轴于点![]() 、
、![]() ,且
,且![]() 为线段
为线段![]() 的中点.
的中点.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)抛物线![]() 的对称轴为
的对称轴为![]() ,顶点为
,顶点为![]() ,在(2)的条件下:
,在(2)的条件下:
①点![]() 为抛物线
为抛物线![]() 对称轴
对称轴![]() 上一动点,当
上一动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标;
的坐标;
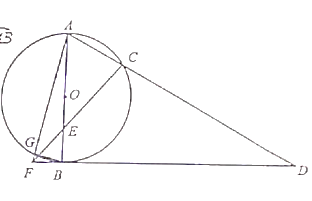
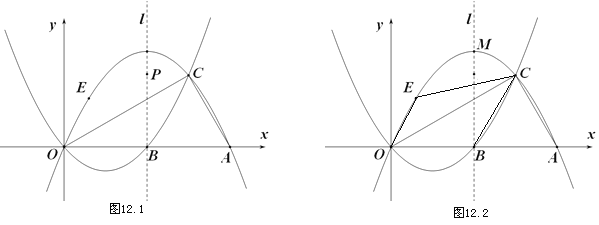
②如图12.2,点![]() 在抛物线
在抛物线![]() 上点
上点![]() 与点
与点![]() 之间运动,四边形
之间运动,四边形![]() 的面积是否存在最大值?若存在,求出面积的最大值和点
的面积是否存在最大值?若存在,求出面积的最大值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①P(
;(3)①P(![]() ,
,![]() );②存在,
);②存在,![]()
【解析】
(1)由两抛物线解析式可分别用a和b表示出A、B两点的坐标,利用B为OA的中点可得到a和b之间的关系式;
(2)由抛物线解析式可先求得C点坐标,过C作CD⊥x轴于点D,可证得△OCD∽△CAD,由相似三角形的性质可得到关于a的方程,可求得OA和CD的长,可求得△OAC的面积;
(3)①连接OC与l的交点即为满足条件的点P,可求得OC的解析式,则可求得P点坐标;
②设出E点坐标,则可表示出△EOB的面积,过点E作x轴的平行线交直线BC于点N,可先求得BC的解析式,则可表示出EN的长,进一步可表示出△EBC的面积,则可表示出四边形OBCE的面积,利用二次函数的性质可求得其最大值,及E点的坐标.
解:
(1)在y=x2+ax中,
当y=0时,x2+ax=0,x1=0,x2=﹣a,
∴B(﹣a,0),
在y=﹣x2+bx中,
当y=0时,﹣x2+bx=0,x1=0,x2=b,
∴A(0,b),
∵B为OA的中点,
∴b=﹣2a,
∴![]() ;
;
(2)联立两抛物线解析式可得: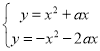 ,
,
消去y整理可得![]() ,
,
解得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
∴C(![]() ,
,![]() ),
),
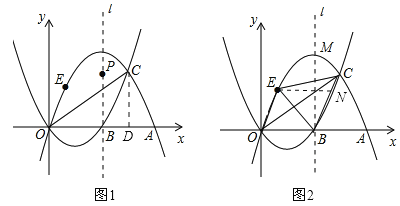
过C作CD⊥x轴于点D,如图1,
∴D(![]() ,0),
,0),
∵∠OCA=90°,
∴△OCD∽△CAD,
∴![]() ,
,
∴CD2=ADOD,即![]() ,
,
∴a1=0(舍去),![]() (舍去),
(舍去),![]() ,
,
∴OA=-2a=![]() ,CD=
,CD=![]() =1,
=1,
∴![]() ;
;
(3)①抛物线![]() ,
,
∴其对称轴![]() ,点A关于l2的对称点为O(0,0),C(
,点A关于l2的对称点为O(0,0),C(![]() ,1),
,1),
则P为直线OC与l2的交点,
设OC的解析式为y=kx,
∴1=![]() k,得k=
k,得k=![]() ,
,
∴OC的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴P(![]() ,
,![]() );
);
②设E(m,![]() )(
)(![]() ),则
),则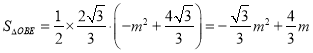 ,
,
而B(![]() ,0),C(
,0),C(![]() ,1),
,1),
设直线BC的解析式为y=kx+b,
由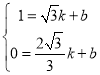 ,解得:k=
,解得:k=![]() ,b=-2,
,b=-2,
∴直线BC的解析式为![]() ,
,
过点E作x轴的平行线交直线BC于点N,如图2,
则![]() ,即x=
,即x=![]()
∴EN=![]()
∴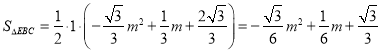
∴S四边形OBCE=S△OBE+S△EBC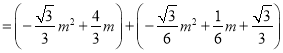
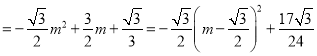 ,
,
![]() ,
,
∴当![]() 时,
时,![]() ,
,
当![]() 时,
时,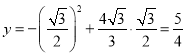 ,
,
∴E(![]() ,
,![]() ),
),![]() .
.